题目内容
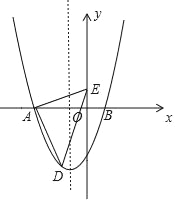
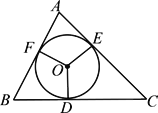
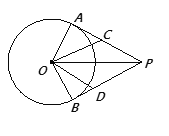
【题目】已知:如图,PA、PB是⊙O的切线;A、B是切点;连结OA、OB、OP.
①若∠COP=∠DOP,求证:AC=BD;
②连结CD,设△PCD的周长为l,若l=2AP,判断直线CD与⊙O的位置关系,并说明理由.
【答案】①详见解析;②直线CD与⊙O相切,理由详见解析.
【解析】
①由(1)知△PAO≌△PBO,得到∠POB=∠POA;再利用AAS判定△AOC≌△BOD,从而得到AC=BD;
②本题要充分利用l=2AP的条件.延长射线PA到F,使AF=BD;易证得△OAF≌△OBD(SAS),得OF=OD;由于l=2AP,即l=PA+PB=PC+PD+CD,因此CD=AC+BD=AC+AF=CF;
在△OCF和△OCD中,OF=OD,OC=OC,FC=CD;可证得△OCF≌△OCD,那么两三角形的对应边上的高也相等,则过O作OE⊥CD,则OE=OA,由此可证得CD与⊙O相切.
①∵∠COP=∠DOP,∠CPO=∠DPO,PO=PO, ∴△OCP≌△ODP,∴CP=DP.
又可证△OPA≌OPB得PA=PB, ∴AC=BD.
②作OE⊥CD于E,设OE=d,CE=x,DE=y. 则d2=AC2+AO2-x2=BD2+OA2-y2.
∴(AC+x)(AC-x)- (BD+y)(BD-y)=0, ∵l=2AP=2BP,∴x+y=AC+BD, ∴AC-x=y-BD.
∴(AC+x)(y-BD)- (BD+y)(BD-y)=0, ∴(y-BD) (AC+x+BD+y)=0.
∵AC+x+BD+y≠0,∴y=BD, 即d=AO,∴直线CD与⊙O相切.

练习册系列答案
相关题目