题目内容
如图点P是矩形ABCD的边AD上的任一点,AB=8, BC=15,则点P到矩形的两条对角线AC和BD的距离之和是____________.
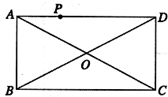


分析:由矩形ABCD可得:S△AOD=
 S矩形ABCD,又由AB=8,BC=15,可求得AC的长,则可求得OA与OD的长,又由S△AOD=S△APO+S△DPO=
S矩形ABCD,又由AB=8,BC=15,可求得AC的长,则可求得OA与OD的长,又由S△AOD=S△APO+S△DPO=  OA?PE+
OA?PE+  OD?PF,代入数值即可求得结果.
OD?PF,代入数值即可求得结果.
解:过点P作PE⊥AC于E,PF⊥BD与F,连接OP,
∵四边形ABCD是矩形,
∴AC=BD,OA=OC=
 AC,OB=OD=
AC,OB=OD= BD,∠ABC=90°,
BD,∠ABC=90°,S△AOD=
 S矩形ABCD,
S矩形ABCD,∴OA=OD=
 AC,
AC,∵AB=8,BC=15,
∴AC=
 =
= =17,S△AOD=
=17,S△AOD= S矩形ABCD=30,
S矩形ABCD=30,∴OA=OD=
 ,
,∴S△AOD=S△APO+S△DPO=
 OA?PE+
OA?PE+ OD?PF=
OD?PF= OA?(PE+PF)=
OA?(PE+PF)= ×
× (PE+PF)=30,
(PE+PF)=30,∴PE+PF=
 .
.∴点P到矩形的两条对角线AC和BD的距离之和是
 .
.故答案为:
 .
.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 中,抛物线
中,抛物线 向左平移1个单位,再向下平移4个单位,得到抛物线
向左平移1个单位,再向下平移4个单位,得到抛物线 .所得抛物线与
.所得抛物线与 轴交于
轴交于 两点(点
两点(点 在点
在点 的左边),与
的左边),与 轴交于点
轴交于点 ,顶点为
,顶点为 .
. 的值;
的值; 上是否存在点
上是否存在点 ,使
,使 与
与 相似.若存在,求出点
相似.若存在,求出点
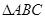 与
与 相似且面积的比为
相似且面积的比为 ,则
,则 若AB=4,S ABCD=
若AB=4,S ABCD=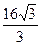 ,求AE的长
,求AE的长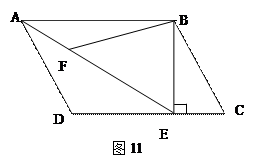

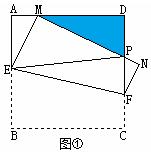
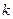 ,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?
,若AD︰BC = 2︰3. 请探究:当k为下列三种情况时,四边形ABPE是什么四边形?

 ,且AB∶
,且AB∶ =1∶2 ,已知BC=8,则
=1∶2 ,已知BC=8,则 的长是( )
的长是( )
