Question

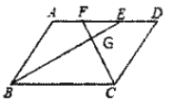
【题目】如图①，在平行四边形OABC中，以O为圆心，OA为半径的圆与BC相切于点B，与OC相交于点D．

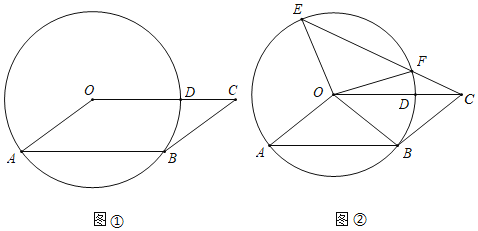
（1）求∠OAB的度数；

（2）如图②，点E在⊙O上，连接CE与⊙O交于点F，若EF＝AB，求∠COE的度数．

Answer 1

【答案】(1) 45°;(2) 105°

【解析】

（1）连接OB，根据BC是圆的切线、四边形OABC是平行四边形得到△AOB是等腰直角三角形，即可求得答案；

（2）作OH⊥EC于点H，设EH＝t，根据四边形OABC是平行四边形得到AB＝CO＝EF＝2t，根据等腰直角三角形的性质可求得半径为t，利用勾股定理可求得OC＝2OH，从而求得∠OCE＝30°，继而求得答案.

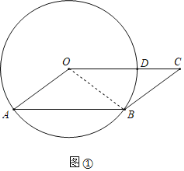
（1）如图①，连接OB，

∵BC是圆的切线，∴OB⊥BC，

∵四边形OABC是平行四边形，

∴OA∥BC，∴OB⊥OA，

∴△AOB是等腰直角三角形，

∴∠OAB＝45°；

（2）如图②，过点O作OH⊥EC于点H，设EH＝t，

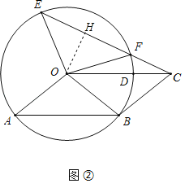
∵OH⊥EC，

∴EF＝2HE＝2t，

∵四边形OABC是平行四边形，

∴AB＝CO＝EF＝2t，

∵△AOB是等腰直角三角形，

∴OA＝t，

则HO＝，

∵OC＝2OH，

∴∠OCE＝30°，

∵HO＝EH＝t且OH⊥EC，

∴∠OEC＝∠EOH＝45°，

∴∠OEC＝180°﹣∠OCE﹣∠OCE＝180°﹣45°﹣30°＝105°．