题目内容
【题目】对x,y定义一种新运算x[]y= ![]() (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= ![]() =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式?
【答案】
(1)
解:①由1[]2=3,﹣1[]3=﹣2,得
![]() ,解得
,解得 ![]() .
.
答:a的值为8,b的值为﹣1.
②把a=8,b=﹣1代入x[]y= ![]() ,得x[]y=
,得x[]y= ![]() ,
,
M=(m2﹣m﹣1)[](2m﹣2m2)=﹣2m2+2m+4=﹣2 ![]() +
+ ![]() ,
,
又∵﹣1≤m≤3,
∴当m= ![]() 时,M取最大值
时,M取最大值 ![]() ;
;
当m=﹣1时,M=0;
当m=3时,M=﹣8.
∴﹣8≤M≤ ![]() =4
=4 ![]() ,
,
∴k=8+4+1=13.
(2)
解:∵x[]y=y[]x,
∴ ![]() =
= ![]() ,
,
∴ay2﹣ax2+4by2﹣4bx2=0,
∴a(y2﹣x2)+4b(y2﹣x2)=0,
即(a+4b)(y2﹣x2)=0.
∵对任意实数x,y都成立,
∴a+4b=0,
∴a=﹣4b
【解析】(1)①结合新运算的定义,代入数据,解二元一次方程组即可得出结论;②将a、b的值代入原定义式中,用m表示出M,由二次函数的性质即可找出M的取值范围,从而得出k的值;(2)x[]y=y[]x得出关于a、b、x、y的等式,由对任意实数x,y都成立,找出恒为0的代数式a+4b=0,从而得出结论.
【考点精析】认真审题,首先需要了解有理数的四则混合运算(在没有括号的不同级运算中,先算乘方再算乘除,最后算加减).

【题目】按下列程序计算,把答案填写在表格内,然后观察有什么规律,想一想:为什么会有这个规律?
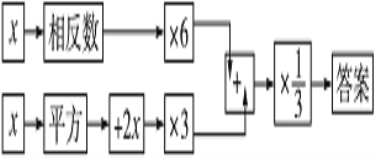
(1)填写表内空格:
输入 | -3 | -2 | -1 | 0 | … |
输出答案 | 9 |
|
|
| … |
(2)发现的规律是:输入数据x,则输出的答案是__________;
(3)为什么会有这个规律?请你说明理由.