题目内容
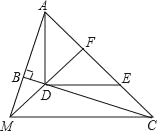
【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
【答案】(1)证明见解析;(2)(2)正确.理由见解析.
【解析】
(1)根据等腰直角三角形的性质,得出DF⊥AE,DF=AF=EF,再证明△DFC≌△AFM,得出FC=FM;
(2)根据等腰三角形的判定,得出FM=FC,再根据等腰三角形的性质,可得MF⊥AC,进而证得△AMF≌△DCF(ASA),最后由全等三角形的性质和直角的关系可证.
(1)证明:∵AD=DE,点F是AE的中点,
∴MF⊥AC,∴∠AMF+∠MAF=90°.
∵∠ABC=90°,∴∠ACB+∠MAF=90°,
∴∠AMF=∠ACB.
∵AD⊥DE,AD=DE,
∴△ADE为等腰直角三角形,∠DAF=45°.
又∵MF⊥AC,∴∠DFA=90°,
∴∠ADF=180°-∠DFA-∠DAF=45°,
∴∠ADF=∠DAF,∴FA=FD.
在△FAM和△FDC中,
∠AMF=∠DCF,∠AFM=∠DFC,FA=FD,
∴△FAM≌△FDC(AAS),
∴FM=FC,∴∠FMC=∠FCM.
(2)解:正确.理由如下:∵∠FMC=∠FCM,∴FM=FC.
∵AD=DE,点F是AE的中点,∴MF⊥AC,
∴∠AFM=∠DFC=90°,∠AMF+∠MAC=90°.
又∵∠MAC+∠DCF=90°,
∴∠AMF=∠DCF.
在△AMF和△DCF中,
∠AMF=∠DCF,FM=FC,∠AFM=∠DFC,
∴△AMF≌△DCF(ASA),
∴AF=DF.
又∵∠AFD=90°,∴∠DAF=∠ADF=45°.
又∵AD=DE,∴∠DEA=∠DAF=45°,
∴∠ADE=180°-∠DAF-∠DEA=90°,
∴AD⊥DE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】甲、乙两果园分别产有苹果10吨和40吨,现全部运送到A、B两地销售,根据市场调研,A、B两地分别需要苹果15吨和35吨;已知从甲、乙地到A、B地的运价如表,由以上信息,解决下列问题:
到A地运价 | 到B地运价 | |
甲果园 | 150元∕吨 | 120元∕吨 |
乙果园 | 100元∕吨 | 90元∕吨 |
(1)若从乙果园运到A地的苹果为![]() 吨,则从甲果园运到B地的苹果为 吨;从甲果园将苹果运往A地的运输费用为 元(用含
吨,则从甲果园运到B地的苹果为 吨;从甲果园将苹果运往A地的运输费用为 元(用含![]() 的代数式表示);
的代数式表示);
(2)若运往A地的运输费用比运往B地的运输费用少1150元,用你所学的知识来说明是怎样安排运输方案的?