题目内容
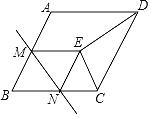
【题目】如图,![]() 是半径为4的
是半径为4的![]() 的内接三角形,连接
的内接三角形,连接![]() ,点
,点![]() 分别是
分别是![]() 的中点.
的中点.
(1)试判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)填空:①若![]() ,当
,当![]() 时,四边形
时,四边形![]() 的面积是__________;②若
的面积是__________;②若![]() ,当
,当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 是正方形.
是正方形.
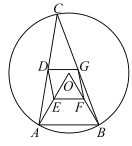
【答案】(1)四边形![]() 是平行四边形,见解析;(2)①6,②75°或15°.
是平行四边形,见解析;(2)①6,②75°或15°.
【解析】
(1)利用中位线性质,中位线平行于第三边并且等于第三边的一半,只要证明DG=EF,DG∥EF即可解决问题;
(2)①只要证明四边形DEFG是矩形即可解决问题;
②分点C在优弧AB或劣弧AB上两种情形讨论即可.
解:
⑴四边形![]() 是平行四边形.
是平行四边形.
∵点![]() 分别是
分别是![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形;
是平行四边形;
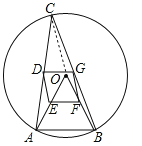
(2)①连接![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴![]() ,同理
,同理![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴四边形![]() 的面积=
的面积=![]() ,故答案为6;
,故答案为6;
②当![]() 是优弧
是优弧![]() 的中点时,四边形
的中点时,四边形![]() 是正方形,此时
是正方形,此时![]() ,
,
当![]() 是劣弧
是劣弧![]() 的中点时,四边形
的中点时,四边形![]() 是正方形,此时
是正方形,此时![]() ,故答案为75°或15°.
,故答案为75°或15°.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
【题目】某村启动“脱贫攻坚”项目,根据当地的地理条件,要在一座高为1000m的上种植一种经济作物.农业技术人员在种植前进行了主要相关因素的调查统计,结果如下:
①这座山的山脚下温度约为22°C,山高h(单位:m)每增加100m,温度T(单位:°C)下降约0.5°C;
②该作物的种植成活率p受温度T影响,且在19°C时达到最大.大致如表:
温度T°C | 21 | 20.5 | 20 | 19.5 | 19 | 18.5 | 18 | 17.5 |
种植成活率p | 90% | 92% | 94% | 96% | 98% | 96% | 94% | 92% |
③该作物在这座山上的种植量w受山高h影响,大致如图1:
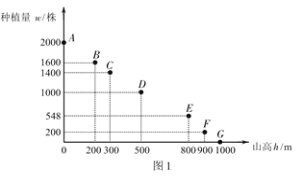
(1)求T关于h的函数解析式,并求T的最小值;
(2)若要求该作物种植成活率p不低于92%,根据上述统计结果,山高h为多少米时该作物的成活量最大?请说明理由.