题目内容
【题目】(1)一个不透明的盒子中装有 2 枚黑色的棋子和 1 枚白色的棋子,每枚棋子除了颜色外其余均相同.从盒中随机摸出一枚棋子,记下颜色后放回并搅匀,再从盒子中随机摸出一枚棋子,记下颜色,用画树状图(或列表)的方法,求两次摸出的棋子颜色不同的概率.
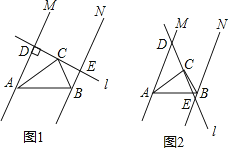
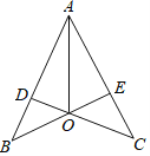
(2)如图,已知 ![]() ,
,![]() ,
,![]() ,
,![]() 交
交![]() 于点O,连接
于点O,连接![]() ,求证:AO平分
,求证:AO平分![]() .
.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与两次摸出的棋子颜色不同的情况,再利用概率公式即可求得答案;
(2)根据已知条件得到△BOD≌△COE,然后得到OD=OE,∠ODB=∠OEC,进而证明△ADO≌△AEO,即可得出答案.
解:(1)画树状图可得:

∵共有9种等可能的结果,两次摸出的棋子颜色不同的有4种情况,
∴两次摸出的棋子颜色不同的概率为:![]() .
.
证明:(2)在△BOD和△COE中

∴△BOD≌△COE(AAS)
∴OD=OE,∠ODB=∠OEC
∠ODA=180°-∠ODB
∠OEA=180°-∠OEC
∴∠ODA=∠OEA
又∵AB=AC,BD=CE
AD=AB-BD
AE=AC-CE
∴AD=AE
在△ADO和△AEO中

∴△ADO≌△AEO(SAS)
∴∠OAD=∠OAE
∴AO平分∠BAC

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目