题目内容
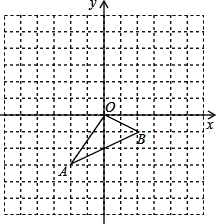
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
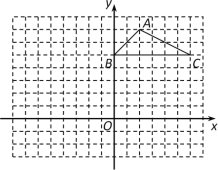
(1) 点A的坐标为 ,点C的坐标为 ;
(2) 将△ABC先向左平移3个单位长度,再向下平移6个单位长度,请画出平移后的△A1B1C1;
(3) 连接A1B,A1 C,△A1BC的面积= .
【答案】(1)(2,7);(6,5);(2)见解析(3)12.
【解析】
(1)直接利用平面直角坐标系得出对应点坐标进而得出答案;
(2)利用平移的性质得出对应点位置进而得出答案;
(3)直接利用三角形面积求法得出答案.
(1)如图所示:A(2,7),C(6,5);
故答案为:(2,7),(6,5);
(2)如图所示:△A1B1C1,即为所求;
(3)△A1BC的面积为:![]() ×6×4=12.
×6×4=12.


【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

【题目】甲、乙两名同学在一次用频率估计概率的实验中,统计了某一个结果出现的频率,绘制了如下的表格,则符合这一结果的实验可能是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1200 |
频率 | 0.430 | 0.360 | 0.320 | 0.328 | 0.330 | 0.329 |
A. 抛一枚质地均匀的硬币,出现正面的概率
B. 从一个装有3个红球和2个白球的不透明袋子里任取1球,取出红球的概率
C. 掷一枚均匀的正方体骰子,出现的点数是3的倍数的概率
D. 从正方形、正五边形、正六边形中任意取一个图形,是轴对称图形的概率