题目内容
【题目】为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
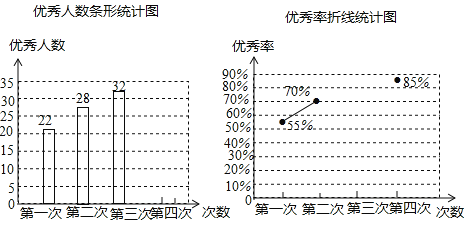
(1)求该班总人数;
(2)根据计算,请你补全两个统计图;
(3)已知该班甲同学四次训练成绩为85,95,85,95,乙同学四次成绩分别为85,90,95,90,现需从甲、乙两同学中选派一名同学参加校级比赛,你认为应该选派哪位同学并说明理由.
【答案】(1)40;(2)见解析;(3)见解析.
【解析】(1)利用折线统计图结合条形统计图,利用优秀人数÷优秀率=总人数求出即可;
(2)分别求出第四次模拟考试的优秀人数以及第三次的优秀率即可得出答案;
(3)答案不唯一.回答合理即可.
(1)由题意可得:该班总人数是:22÷55%=40(人);
(2)由(1)得:第四次优秀的人数为:40×85%=34(人),第三次优秀率为:![]() ×100%=80%;
×100%=80%;
如图所示:
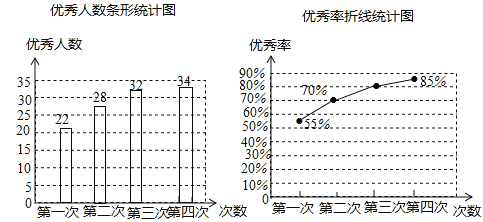 ;
;
(3)答案不唯一.如:选乙,理由甲乙平均分相同都是90分,但![]() ,乙成绩稳(选甲,理由甲乙平均分相同都是90分,但甲的众数是85,95,更易冲击高分)回答合理即可.
,乙成绩稳(选甲,理由甲乙平均分相同都是90分,但甲的众数是85,95,更易冲击高分)回答合理即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目