题目内容
【题目】如图所示,直线AM∥BN,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA,NB分别相交于点D,E.
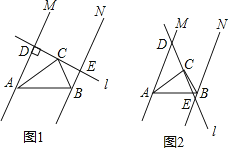
(1)如图1,当直线l与直线MA垂直时,试探究AB,AD,BE之间的数量关系并说明理由;
(2)如图2,当直线l与直线MA不垂直,且交点D,E在AB的异侧时,则(1)的结论还成立吗?若成立,请说明理由;若不成立,请直接写出AB,AD,BE之间的数量关系.
【答案】(1)AD+BE=AB(2)不成立,ADAB=BE.
【解析】
(1)延长AC交BE于Q,求出AB=BQ,根据等腰三角形性质求出AC=CQ,推出AD=EQ,即可得出答案.
(2)延长AC交NB于点F,同①可得AB=BF,再由全等三角形的判定定理得出△ACD≌△FCE,故可得出AD=EF,由此可得出结论.
解:(1)AB=AD+BE;理由如下:
延长AC交BE于Q,如图1所示:
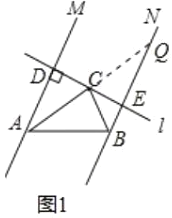
∵AC平分∠MAB,
∴∠MAC=∠BAC,
∵AM∥BN,
∴∠MAC=∠AQB,
∴∠BAC=∠AQB,
∴AB=BQ,
∵BC平分∠ABN,
∴AC=CQ,
∵AM∥BN,
∴△ACD∽△QCE,
∴![]()
∴AD=EQ,
∴AD+BE=AB.
(2)(1)的结论不成立,ADAB=BE.理由如下:
延长AC交BE于点F,如图2所示:
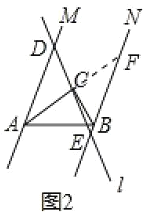
∵AM∥BN,
∴∠MAC=∠AFB.
∵AC是∠MAB的平分线,
∴∠MAC=∠BAC,
∴∠BAC=∠AFB,
∴AB=BF.
∵AC⊥BC,
∴AC=CF.
∵AM∥BN,
∴∠DAC=∠EFC,
在△ACD与△FCE中,
 ,
,
∴△ACD≌△FCE(ASA),
∴AD=EF,
∴ADAB=BE.

【题目】甲、乙两名同学在一次用频率估计概率的实验中,统计了某一个结果出现的频率,绘制了如下的表格,则符合这一结果的实验可能是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1200 |
频率 | 0.430 | 0.360 | 0.320 | 0.328 | 0.330 | 0.329 |
A. 抛一枚质地均匀的硬币,出现正面的概率
B. 从一个装有3个红球和2个白球的不透明袋子里任取1球,取出红球的概率
C. 掷一枚均匀的正方体骰子,出现的点数是3的倍数的概率
D. 从正方形、正五边形、正六边形中任意取一个图形,是轴对称图形的概率