题目内容
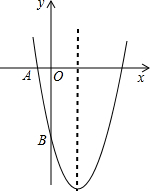
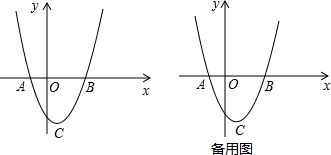
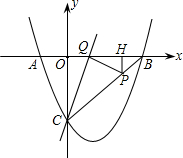
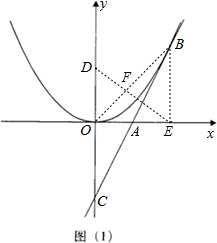
如图(1),直线y=kx-k2(k为常数,且k>0)与y轴交于点C,与抛物线y=ax2有唯一公共点B,点B在x轴上的正投影为点E,已知点D(0,4).
(1)求抛物线的解析式;
(2)是否存在实数k,使经过D,O,E三点的圆与抛物线的交点恰好为B?若存在,请求出时k的值;若不存在,请说明理由.
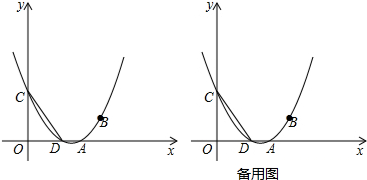
(3)如图(2),连接CE,已知点F(0,1),直线FA与CE相交于点M,不论k取何值,在①∠EAM=∠ECA,②∠EAM=∠ACF两个等式中有一个恒成立.请判断哪一个恒成立,并证明这个成立的结论.

(1)求抛物线的解析式;
(2)是否存在实数k,使经过D,O,E三点的圆与抛物线的交点恰好为B?若存在,请求出时k的值;若不存在,请说明理由.
(3)如图(2),连接CE,已知点F(0,1),直线FA与CE相交于点M,不论k取何值,在①∠EAM=∠ECA,②∠EAM=∠ACF两个等式中有一个恒成立.请判断哪一个恒成立,并证明这个成立的结论.

(1)∵直线y=kx-k2与抛物线y=ax2有唯一公共点B,
∴kx-k2=ax2,即ax2-kx+k2=0有两个相等的实数根,
∴(-k)2-4ak2=0,而k>0,
∴a=
,
∴y=
x2;
(2)存在实数k,使得经过D、O、E三点的圆与抛物线的交点刚好为点B,
∵
的解为
,
∴点B的坐标为(2k,k2),
又∵点B在x轴上的正投影为点E,连接BE,
则BE⊥x轴于E,
∴E(2k,0),
∴DE⊥OB,DF=EF=OF,
连接OB、DE,则OB、DE均为过点D、0、E三点的圆的直径,
∴Rt△ODE≌Rt△EBO(HL),
∴BE=DO,
∵D(0,4),
∴k2=4,
∴k=2(k>0);
(3)结论②∠EAM=∠ACF成立,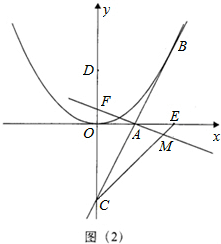
对y=kx-k2,令y=0,得x=k,
∴A(k,0),
∴OA=k,
令x=0,得y=-k2,
∴C(0,-k2),
∴OC=k2,
又∵F(0,1),
∴OF=1,
∴OA2=OF•OC,
∴
=
,
又∵∠FOA=∠AOC=90°,
∴△AFO∽△CAO,
∴∠FAO=∠ACF,而∠FAO=∠EAM,
∴∠EAM=∠ACF.
∴kx-k2=ax2,即ax2-kx+k2=0有两个相等的实数根,
∴(-k)2-4ak2=0,而k>0,
∴a=
| 1 |
| 4 |
∴y=
| 1 |
| 4 |
(2)存在实数k,使得经过D、O、E三点的圆与抛物线的交点刚好为点B,
∵
|
|
∴点B的坐标为(2k,k2),
又∵点B在x轴上的正投影为点E,连接BE,
则BE⊥x轴于E,
∴E(2k,0),
∴DE⊥OB,DF=EF=OF,
连接OB、DE,则OB、DE均为过点D、0、E三点的圆的直径,
∴Rt△ODE≌Rt△EBO(HL),
∴BE=DO,
∵D(0,4),
∴k2=4,
∴k=2(k>0);
(3)结论②∠EAM=∠ACF成立,

对y=kx-k2,令y=0,得x=k,
∴A(k,0),
∴OA=k,
令x=0,得y=-k2,
∴C(0,-k2),
∴OC=k2,
又∵F(0,1),
∴OF=1,
∴OA2=OF•OC,
∴
| OA |
| OF |
| OC |
| OA |
又∵∠FOA=∠AOC=90°,
∴△AFO∽△CAO,
∴∠FAO=∠ACF,而∠FAO=∠EAM,
∴∠EAM=∠ACF.


练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目