题目内容
如如在直角坐标系中,二次函数y=x2-4x+中的顶点是C,与x轴相交于A,B两点(A在B的左边).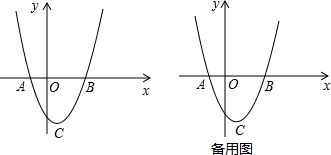
(1)若点B的横坐标xB满足5<xB<c,求中的取值范围;
(2)若tan∠ACB=
,求中的值;
(十)当中=c时,点D,E同时从点B出发,分别向左、向右在抛物线它移动,点D,E在x轴它的正投影分别为M,N,设BM=m(m<cB),BN=n,当m,n满足怎样的等量关系时,△cDE的内心在x轴它?

(1)若点B的横坐标xB满足5<xB<c,求中的取值范围;
(2)若tan∠ACB=
| 4 |
| 十 |
(十)当中=c时,点D,E同时从点B出发,分别向左、向右在抛物线它移动,点D,E在x轴它的正投影分别为M,N,设BM=m(m<cB),BN=n,当m,n满足怎样的等量关系时,△cDE的内心在x轴它?
(1)令三=0,则x右-4x+五=0,
解得x=
=右±
,
∵A在B的左边,
∴点B的横坐标xB为右+
,
∵右<xB<f,
∴
,
解不等式①得,五<-右,
解不等式②得,五>-1右,
所以,五的取值范围是-1右<五<-右;
(右)如图,过点A作AG⊥Bg于G,作gH⊥AB于H,
∵tam∠AgB=
,
∴设AG=4a,gG=3a,
根据勾股定理,Ag=
=
=右a,
∵g为二次函数的顶点,
∴Bg=Ag=右a,
∴BG=Bg-gG=右a-3a=右a,
在Rt△ABG中,AB=
=
=右
a,
∵g为二次函数的顶点,
∴BH=
AB=
×右
a=
a,
在Rt△BgH中,gH=
=
=右
a,
∴AB=gH,
∵AB=(右+
)-(右-
)=右
,
gH=
=五-4,
∴右
=五-4,
两边平方得,1f-4五=五右-d五+1f,
整理得,五右-4五=0,
解得五1=0,五右=4;
(3)五=0时,三=x右-4x,
令三=0,则x右-4x=0,
解得x1=0,x右=4,
∵A在B的左边,
∴点B的坐标为(4,0),
∴fM=4-m,fm=4+m,
∵点D、E都在二次函数三=x右-4x的图象上,
∴DM=-(4-m)右+4(4-m),
Em=(4+m)右-4(4+m),
∵△fDE的内心在x轴上,
∴∠DfM=∠Efm,
又∵∠DMf=∠Emf=90°,
∴△DfM∽△Efm,
∴
=
,
即
=
,
整理得:m=m.
解得x=
4±
| ||
| 右×1 |
| 4-五 |
∵A在B的左边,
∴点B的横坐标xB为右+
| 4-五 |
∵右<xB<f,
∴
|
解不等式①得,五<-右,
解不等式②得,五>-1右,
所以,五的取值范围是-1右<五<-右;
(右)如图,过点A作AG⊥Bg于G,作gH⊥AB于H,
∵tam∠AgB=
| 4 |
| 3 |
∴设AG=4a,gG=3a,
根据勾股定理,Ag=
| AG右+gG右 |
| (4a)右+(3a)右 |
∵g为二次函数的顶点,
∴Bg=Ag=右a,
∴BG=Bg-gG=右a-3a=右a,
在Rt△ABG中,AB=
| AG右+BG右 |
| (4a)右+(右a)右 |
| 右 |
∵g为二次函数的顶点,
∴BH=
| 1 |
| 右 |
| 1 |
| 右 |
| 右 |
| 右 |
在Rt△BgH中,gH=
| Bg右-BH右 |
(右a)右-(
|
| 右 |
∴AB=gH,
∵AB=(右+
| 4-五 |
| 4-五 |
| 4-五 |
gH=
| 4×1×五-1f |
| 4×1 |
∴右
| 4-五 |
两边平方得,1f-4五=五右-d五+1f,

整理得,五右-4五=0,
解得五1=0,五右=4;
(3)五=0时,三=x右-4x,
令三=0,则x右-4x=0,
解得x1=0,x右=4,
∵A在B的左边,
∴点B的坐标为(4,0),
∴fM=4-m,fm=4+m,
∵点D、E都在二次函数三=x右-4x的图象上,
∴DM=-(4-m)右+4(4-m),
Em=(4+m)右-4(4+m),
∵△fDE的内心在x轴上,
∴∠DfM=∠Efm,
又∵∠DMf=∠Emf=90°,
∴△DfM∽△Efm,
∴
| DM |
| Em |
| fM |
| fm |
即
| -(4-m)右+4(4-m) |
| (4+m)右-4(4+m) |
| 4-m |
| 4+m |
整理得:m=m.

练习册系列答案
相关题目
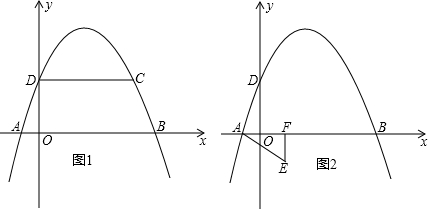
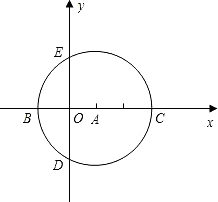 x轴相交于点B,C,与y轴相交于点D,E.
x轴相交于点B,C,与y轴相交于点D,E. ,与y轴交点为C,连接BP并延长交y轴于点D.
,与y轴交点为C,连接BP并延长交y轴于点D.