Question

【题目】如图，在平面直角坐标系中，过点B（6，0）的直线AB与直线OA相交于点A（4，2）.

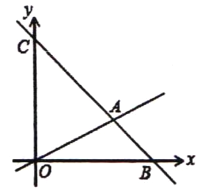
（1）求直线AB的解析式.

（2）求△OAC的面积.

（3）在y轴的负半轴上是否存在点M，使△ABM是以AB为直角边的直角角形？如果存在，求出点M的坐标；如果不存在，说明理由.

Answer 1

【答案】（1）y=﹣x+6；（2）12；（3）点M的坐标为（0，-2）或（0，-6）.

【解析】（1）利用待定系数法即可求得函数的解析式；

（2）求得C的坐标，即OC的长，利用三角形的面积公式即可求解；

（3）分两种情形①过点A作AB的垂线AM交y轴与M．②过点B作BM′⊥AB交y轴与M′，求出点M与M′坐标即可．

（1）设直线AB的解析式是y=kx+b，

根据题意得：，

解得：，

则直线的解析式是：y=-x+6；

（2）在y=-x+6中，令x=0，解得：y=6，

S△OAC=×6×4=12；

（3）如图，

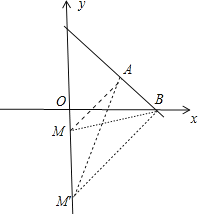
①过点A作AB的垂线AM交y轴与M．

∵直线AB的解析式为y=-x+6，

∴直线AM的解析式为y=x-2，

∴M（0，-2）．

②过点B作BM′⊥AB交y轴与M′，则直线BM′的解析式为y=x-6，

∴M′（0，-6），

综上所述，满足条件的点M的坐标为（0，-2）或（0，-6）．