题目内容
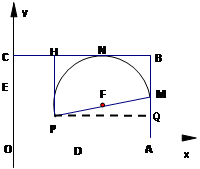
如图,在平面直角坐标系中,四边形OABC是矩形,OA = 6,AB = 4,直线y =" -" x +3与坐标轴交于D、E。设M是AB的中点,P是线段DE上的动点.
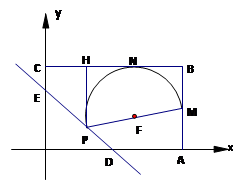
(1)求M、D两点的坐标;
(2)当P在什么位置时,PA = PB?求出此时P点的坐标;
(3)过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,求梯形PMBH的面积.

(1)求M、D两点的坐标;
(2)当P在什么位置时,PA = PB?求出此时P点的坐标;
(3)过P作PH⊥BC,垂足为H,当以PM为直径的⊙F与BC相切于点N时,求梯形PMBH的面积.
解:(1)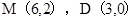

(2)∵PA=PB,∴点P在线段AB的中垂线上,
∴点P的纵坐标是2,又∵点P在y=-x+3上,
∴点P的坐标为(1,2)·
(3)设P(x,y) ∵点P在y=-x+3上,
∵点P在y=-x+3上,
∴P(x, -x+3),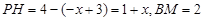
连结NF.FN⊥BC,F是圆心.
∴N是线段HB的中点,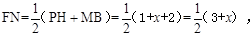
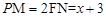 。
。
过P作PQ⊥AB于Q,
则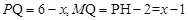 ,在Rt△PQM中, PM2= PQ2 +QM2,即
,在Rt△PQM中, PM2= PQ2 +QM2,即 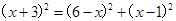 ,化简得:
,化简得: 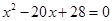 ,·
,·
解得: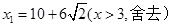 ,
,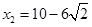 ·
·
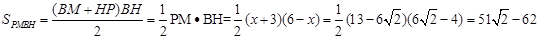
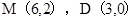

(2)∵PA=PB,∴点P在线段AB的中垂线上,
∴点P的纵坐标是2,又∵点P在y=-x+3上,
∴点P的坐标为(1,2)·
(3)设P(x,y)
 ∵点P在y=-x+3上,
∵点P在y=-x+3上,∴P(x, -x+3),
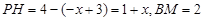
连结NF.FN⊥BC,F是圆心.
∴N是线段HB的中点,
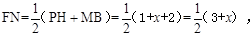
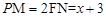 。
。过P作PQ⊥AB于Q,

则
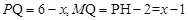 ,在Rt△PQM中, PM2= PQ2 +QM2,即
,在Rt△PQM中, PM2= PQ2 +QM2,即 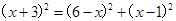 ,化简得:
,化简得: 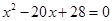 ,·
,·解得:
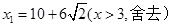 ,
,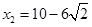 ·
·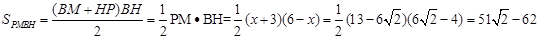
(1)因为四边形OABC是矩形,OA=4,AB=2,直线y="-x+3" ,与坐标轴交于D、E,M是AB的中点,所以令y=0,即可求出D的坐标,而AM=2,所以M(6,2);
(2)因为PA=PB,所以P是AB的垂直平分线和直线ED的交点,而AB的中垂线是y=2,所以P的纵坐标为2,令直线ED的解析式中的y=2,求出的x的值即为相应的P的横坐标;
(3)可设P(x,y),连接PN、MN、NF,因为点P在y="-x+3" 上,所以P(x,-x+3 ), 可得到关于x的方程,解之即可求出x的值,而所求面积的四边形是一个直角梯形,所以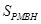 =
=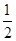 (BM+HP)•BH
(BM+HP)•BH
(2)因为PA=PB,所以P是AB的垂直平分线和直线ED的交点,而AB的中垂线是y=2,所以P的纵坐标为2,令直线ED的解析式中的y=2,求出的x的值即为相应的P的横坐标;
(3)可设P(x,y),连接PN、MN、NF,因为点P在y="-x+3" 上,所以P(x,-x+3 ), 可得到关于x的方程,解之即可求出x的值,而所求面积的四边形是一个直角梯形,所以
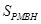 =
=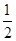 (BM+HP)•BH
(BM+HP)•BH 
练习册系列答案
相关题目

 cm2的扇形纸片,现需要一个半径为
cm2的扇形纸片,现需要一个半径为 的圆形纸片,使两张纸片刚好能组合成圆锥体,则
的圆形纸片,使两张纸片刚好能组合成圆锥体,则
 到水面
到水面 距离
距离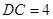 米.
米.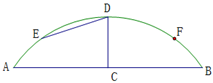
 时,从点
时,从点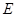 测得桥顶
测得桥顶 ,若
,若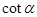 =3,求水面上升的高度.
=3,求水面上升的高度.