题目内容
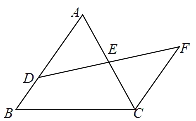
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 的切线,
的切线,![]() ,交
,交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 的中点,连接
的中点,连接![]() ,交
,交![]() 于点
于点![]() .
.
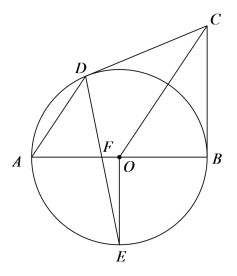
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,求
,求![]() .
.
【答案】(1)详见解析;(2)详见解析;(3)![]()
【解析】
(1)连接OD,根据平行线的性质和等腰三角形的性质,得出相等的边和角,然后判断出△CDO≌△CBO,判断出∠CDO是直角即可解决.
(2)根据圆周角定理的推论,判断出∠ADB为90°,再结合平行线的性质得出相等的角,根据相似三角形的判定方法证明△ABD∽△OCB,然后根据相似三角形的性质列出比例式,将比例式变形即可解决.
(3)过点D向AB作垂线,设![]() ,根据射影定理,得出AG的长度,计算出OG的长度,根据勾股定理计算出DG的长度,由垂径定理得出∠AOE的度数,然后结合平行线的性质得出相似三角形,列出比例式,即可解决.
,根据射影定理,得出AG的长度,计算出OG的长度,根据勾股定理计算出DG的长度,由垂径定理得出∠AOE的度数,然后结合平行线的性质得出相似三角形,列出比例式,即可解决.
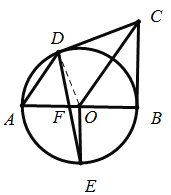
(1)连接![]() ,
,
![]() 为⊙
为⊙![]() 的切线,
的切线,![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
即![]() .
.
![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)连接![]() ,
,
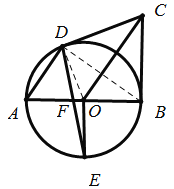
![]() 为⊙
为⊙![]() 的直径,
的直径,
![]() .
.
又![]() ,
,
![]() .
.
![]() .
.
![]() ,
,
又∵AB=2OB=2OA,OA=OB,
∴![]() ;
;
(3)作![]() ,垂足为
,垂足为![]() ,设
,设![]() .
.
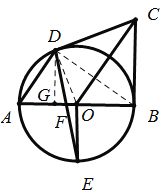
![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
 .
.
![]() 为
为![]() 的中点,
的中点,
![]() ,
,
![]() .
.
![]() ,
,
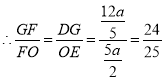 .
.
![]() .
.
 .
.

练习册系列答案
相关题目