题目内容
【题目】问题提出
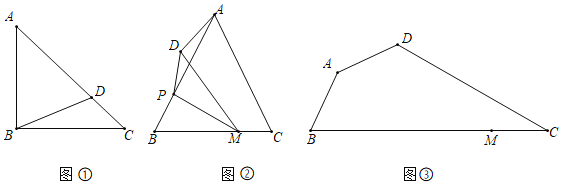
(1)如图①,在等腰Rt△ABC中,斜边AC=4,点D为AC上一点,连接BD,则BD的最小值为 ;
问题探究
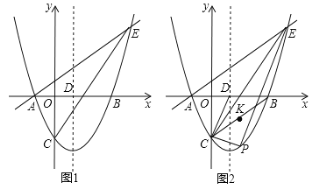
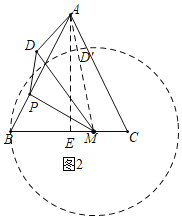
(2)如图②,在△ABC中,AB=AC=5,BC=6,点M是BC上一点,且BM=4,点P是边AB上一动点,连接PM,将△BPM沿PM翻折得到△DPM,点D与点B对应,连接AD,求AD的最小值;
问题解决
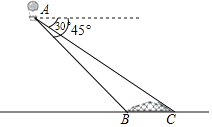
(3)如图③,四边形ABCD是规划中的休闲广场示意图,其中∠BAD=∠ADC=135°,∠DCB=30°,AD=2![]() km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
km,AB=3km,点M是BC上一点,MC=4km.现计划在四边形ABCD内选取一点P,把△DCP建成商业活动区,其余部分建成景观绿化区.为方便进入商业区,需修建小路BP、MP,从实用和美观的角度,要求满足∠PMB=∠ABP,且景观绿化区面积足够大,即△DCP区域面积尽可能小.则在四边形ABCD内是否存在这样的点P?若存在,请求出△DCP面积的最小值;若不存在,请说明理由.
【答案】(1)2;(2)![]() ;(3) 存在点P,使得△DCP的面积最小,△DCP面积的最小值是(
;(3) 存在点P,使得△DCP的面积最小,△DCP面积的最小值是(![]() ﹣20)km2.
﹣20)km2.
【解析】
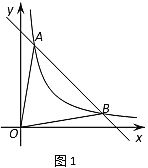
(1)如图1,当BD⊥AC时,BD的值最小,根据直角三角形斜边中线的性质可得结论;
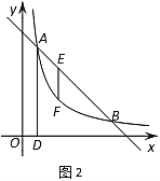
(2)如图2,根据BM=DM可知:点D在以M为圆心,BM为半径的⊙M上,连接AM交⊙M于点D',此时AD值最小,计算AM和半径D'M的长,可得AD的最小值;
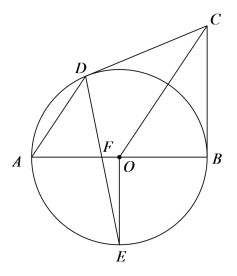
(3)如图3,先确定点P的位置,再求△DCP的面积;假设在四边形ABCD中存在点P,以BM为边向下作等边△BMF,可知:A、F、M、P四点共圆,作△BMF的外接圆⊙O,圆外一点与圆心的连线的交点就是点P的位置,并构建直角三角形,计算CD和PQ的长,由三角形的面积公式可求得面积.
解:(1)当BD⊥AC时,如图1,

∵AB=BC,
∴D是AC的中点,
∴BD=![]() AC=
AC=![]() ×4=2,即BD的最小值是2;
×4=2,即BD的最小值是2;
故答案为2;
(2)如图2,由题意得:DM=MB,
∴点D在以M为圆心,BM为半径的⊙M上,连接AM交⊙M于点D',此时AD值最小,
过A作AE⊥BC于E,
∵AB=AC=5,
∴BE=EC=![]() BC=
BC=![]() ,
,
由勾股定理得:AE=![]() 4,
4,
∵BM=4,
∴EM=4﹣3=1,
∴AM=![]() ,
,
∵D'M=BM=4,
∴AD'=AM﹣D'M=![]() ﹣4,
﹣4,
即线段AD长的最小值是![]() ﹣4;
﹣4;
(3)如图3,假设在四边形ABCD中存在点P,
∵∠BAD=∠ADC=135°,∠DCB=30°,
∴∠ABC=360°﹣∠BAD﹣∠ADC﹣∠DCB=60°,
∵∠PMB=∠ABP,
∴∠BPM=180°﹣∠PBM﹣∠PMB=180°﹣(∠PBM+∠ABP)=180°﹣∠ABC=120°,
以BM为边向下作等边△BMF,作△BMF的外接圆⊙O,

∵∠BFM+∠BPM=60°+120°=180°,则点P在![]() 上,
上,
过O作OQ⊥CD于Q,交⊙O于点P,
设点P'是![]() 上任意一点,连接OP',过P'作P'H⊥CD于H,
上任意一点,连接OP',过P'作P'H⊥CD于H,
可得OP'+P'H≥OQ=OP+PQ,即P'H≥PQ,
∴P即为所求的位置,
延长CD,BA交于点E,
∵∠BAD=∠ADC=135°,∠DCB=30°,∠ABC=60°,
∴∠E=90°,∠EAD=∠EDA=45°,
∵AD=2![]() ,
,
∴AE=DE=2,
∴BE=AE+AB=5,BC=2BE=10,CE=5![]() ,
,
∴BM=BC﹣MC=6,CD=5![]() ﹣2,
﹣2,
过O作OG⊥BM于G,
∵∠BOM=2∠BFM=120°,OB=OM,
∴∠OBM=30°,
∴∠ABO=∠ABM+∠MBO=90°,OB![]() =2
=2![]() ,
,
∴∠E=∠ABO=∠OQE=90°,
∴四边形OBEQ是矩形,
∴OQ=BE=5,
∴PQ=OQ﹣OP=5﹣2![]() ,
,
∴S△DPC=![]() ﹣20,
﹣20,
∴存在点P,使得△DCP的面积最小,△DCP面积的最小值是(![]() ﹣20)km2.
﹣20)km2.