��Ŀ����
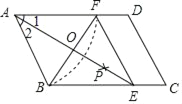
����Ŀ����ͼ����ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BF�ij�Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
BF�ij�Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��1��������������ͼ��Ϣ֪�ı���ABEF���� ��
A���������ƽ���ı���
B������
C������
D��������
��2����AE��BF�ཻ�ڵ�O���ı���ABEF���ܳ�Ϊ16��BF=4����AE�ij��͡�C�Ķ�����
���𰸡���1��C����2��60��
��������
��1��������ͼ����֪����ȷ�����ı���ABEF����״���ɣ�
��2������������������BE�ij������ù��ɶ������OE�ij����̶����AE�ij����õ�������BEFΪ�ȱ������Σ�������ƽ���ı��ε����ʼ����������
��1��������������ͼ��Ϣ֪�ı���ABEF�����Σ�
��ѡC��
��2�����ı���ABEF�����Σ�
��AE��BF��OB=OF��
��BF=4��
��![]()
���ı���ABEF���ܳ�Ϊ16��
��BE=4��
��Rt��OBE�У����ݹ��ɶ����ã�![]()
��![]()
��BE=BF=EF=4��
���BEF�ǵȱ������Σ�
���FEB=60�㣬
���ı���ABCD��ƽ���ı��Σ�
��AB��EF��
��AB��CD��
��CD��EF��
���C=��BEF=60�㣮

��ϰ��ϵ�д�
�����Ŀ