题目内容
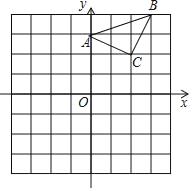
【题目】如图，抛物线y=ax2+bx+c经过A（﹣5，0），B（1，0），C（0，
）三点
（1）填空：抛物线的解析式是 ；
（2）①在抛物线的对称轴上有一点P，使PB+PC的值最小，求点P的坐标；
②点M为x轴上一动点，在抛物线上是否存在一点N，使以B，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．
【答案】（1）y=﹣
x -2x+
；（2）①点P的坐标是（﹣2，
）;②存在 ，满足题目条件的点N共有三个，分别为（﹣4，），（﹣2+
，﹣）和（﹣2﹣，﹣）．
.
【解析】
（1）设抛物线的解析式为y=a（x+5）（x﹣1），再把C（0，）代入求出a的值，整理即可求得抛物线的解析式；（2）连接AC交抛物线的对称轴于点P，则P点即为所求，用待定系数法求得直线AC的解析式，由此即可求得点P的坐标；（3）分点N在x轴下方或上方两种情况求点N的坐标即可.
（1）设抛物线的解析式为：y=a（x+5）（x﹣1），
把（0，
）代入得：﹣5a=，a=﹣
，
∴抛物线的解析式是：y=﹣x -2x+；
故答案为： y=﹣x -2x+；
（2）①由题意知，点B关于抛物线对称轴的对称点为点A，如图1，连接AC交抛物线的对称轴于点P，则P点即为所求．
设直线AC的解析式为：y=kx+b，由题意，得
，解得
，
∴直线AC的解析式为：y=
x+
，
∵抛物线：y=﹣
=﹣（x﹣2）2+
，
∴对称轴是x=﹣2，
∴当x=﹣2时，y=
x+
=
，
∴点P的坐标是（﹣2，）．
②存在
（ i）当存在的点N在x轴的上方时，如图2所示，
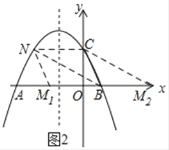
∵四边形BCNM1或四边形CNBM2是平行四边形，
∴CN∥x轴，
∴点C与点N关于对称轴x=﹣2对称，
∵C点的坐标为（0，），
∴点N的坐标为（﹣4，）
（ II）当存在的点N在x轴下方时，如图3所示，作NH⊥x轴于点H，
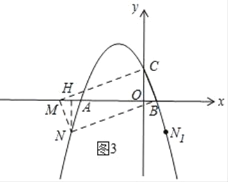
∵四边形BCMN是平行四边形，
∴BC=MN，∠NMH=∠CBO，
∴Rt△CBO≌Rt△NMH，
∴NH=OC．
∵点C的坐标为（0，），
∴NH=
，即N点的纵坐标为﹣，
∴﹣
=﹣即x2+4x﹣10=0，
解得
（就是点N1），
，
∴点N的坐标为（﹣2+
，﹣）和（﹣2﹣
，﹣）．
综上所述，满足题目条件的点N共有三个，分别为（﹣4，），（﹣2+，﹣）和（﹣2﹣，﹣）．
