题目内容
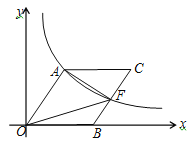
【题目】如图,O为坐标原点,点B在x轴的正半轴上,四边形OACB是平行四边形,OA =10,sin∠AOB =![]() ,反比例函数y =kx-1(k>0)在第一象限内的图象经过点A,与BC交于点F.
,反比例函数y =kx-1(k>0)在第一象限内的图象经过点A,与BC交于点F.
(1)求反比例函数的表达式;
(2)若点F为BC的中点,求△OBF的面积.
【答案】(1)y=![]() (x>0);(2)18
(x>0);(2)18
【解析】(1)先过点A作AH⊥OB,根据sin∠AOB=![]() ,OA=10,求出AH和OH的值,从而得出A点坐标,再把它代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
,OA=10,求出AH和OH的值,从而得出A点坐标,再把它代入反比例函数中,求出k的值,即可求出反比例函数的解析式;
(2)过点F作FM⊥x轴于M,由四边形AOBC是平行四边形得∠AOB=∠FBM,故sin∠FBM=![]() ,因点F为BC的中点,所以BF=5,得FM=4,BM=3,得S△BFM=6,因为点F在反比例函数图象上,故S△OFM=24,根据S△OBF=S△OFM-S△BFM可求出结果.
,因点F为BC的中点,所以BF=5,得FM=4,BM=3,得S△BFM=6,因为点F在反比例函数图象上,故S△OFM=24,根据S△OBF=S△OFM-S△BFM可求出结果.
(1)过点A作AH⊥OB于H
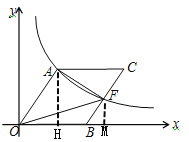
∵sin∠AOB=![]() ,OA=10
,OA=10
∴AH=8,OH=6
∴A点坐标为(6,8)
∵反比例函数y=kx(k>0)过(3,4)
可得:k=48
∴反比例函数解析式:y=![]() (x>0)
(x>0)
(2)过点F作FM⊥x轴于M
∵四边形AOBC是平行四边形,
∴AO∥BC,AO=CB=10 ∴∠AOB=∠FBM
∵sin∠AOB=![]()
∴sin∠FBM=![]()
∵点F为BC的中点,
∴BF=5,
∴FM=4,BM=3,
∴S△BFM=6
∵F在反比例函数图象上,
∴S△OFM=24
∴S△OBF=S△OFM-S△BFM=18

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目