题目内容
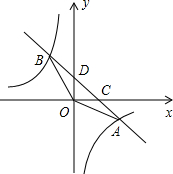
如图,一次函数y=ax+b(b≠0)的图象与反比例函数y=
的图象交于A,B两点,与x轴交于点C,与y轴交于点D,已知OA=
,tan∠AOC=
,且S△AOD=1.
(1)求反比例函数和一次函数的解析式;
(2)求△OAB的面积.
| k |
| x |
| 5 |
| 1 |
| 2 |
(1)求反比例函数和一次函数的解析式;
(2)求△OAB的面积.

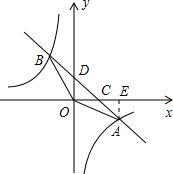
(1)过A作AE⊥x轴,交x轴于点E,
在Rt△AOE中,OA=
,tan∠AOC=
,
设AE=m,则OE=2m,
根据勾股定理得:OA2=OE2+AE2,即m2+4m2=5,
解得:m=1或m=-1(舍去),
∴AE=1,OE=2,即A(2,-1),
将x=2,y=-1代入反比例解析式得:-1=
,
解得:k=-2,
∴反比例解析式为y=-
;
∵S△AOD=
OD•OE=1,OE=2,
∴OD=1,即D(0,1),
将A和D坐标代入y=ax+b中得:
,
解得:
,
则一次函数解析式为y=-x+1;
(2)对于一次函数y=-x+1,
令y=0,求得x=1,故C(1,0),即OC=1,
将一次函数与反比例函数联立得:
,
解得:
或
,
∴B(-1,2),
则S△AOB=S△BOC+S△AOC=
×1×2+
×1×1=
.
在Rt△AOE中,OA=
| 5 |
| 1 |
| 2 |
设AE=m,则OE=2m,
根据勾股定理得:OA2=OE2+AE2,即m2+4m2=5,
解得:m=1或m=-1(舍去),
∴AE=1,OE=2,即A(2,-1),
将x=2,y=-1代入反比例解析式得:-1=
| k |
| 2 |
解得:k=-2,
∴反比例解析式为y=-
| 2 |
| x |
∵S△AOD=
| 1 |
| 2 |
∴OD=1,即D(0,1),
将A和D坐标代入y=ax+b中得:
|
解得:
|
则一次函数解析式为y=-x+1;
(2)对于一次函数y=-x+1,
令y=0,求得x=1,故C(1,0),即OC=1,
将一次函数与反比例函数联立得:
|
解得:
|
|
∴B(-1,2),
则S△AOB=S△BOC+S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
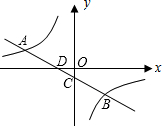


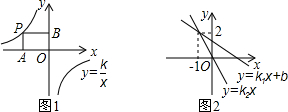 平面直角坐标系中的图象如图2所示,则关于x的不等式k1x+b>k2x的解为______.
平面直角坐标系中的图象如图2所示,则关于x的不等式k1x+b>k2x的解为______.