Question

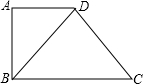
如图，在梯形ABCD中，AB∥DC，AB⊥BC，E是AD的中点，AB+BC+CD=6，BE=

5

，则梯形ABCD的面积等于（　　）

A．13

B．8

C． 13 2

D．4

Answer 1

如图，过点E作EF∥AB交BC于点F，
则BF=

1

2

BC，EF=

1

2

（AB+CD）=

1

2

（6-BC），
又∵AB⊥BC，
∴EF⊥BC，
∴在Rt△BFE中，EF²+BF²=BE²．
∴[

1

2

(6-BC)]2+(

1

2

BC)2=(

5

)2，即BC²-6BC+8=0，
解得BC=2或BC=4，则EF=2或EF=1，
∴S_梯形ABCD=EF•BC=4．
故选D．