Question

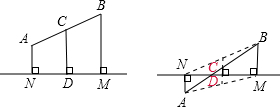
在平面内有线段AB和直线l，点A、B到直线l的距离分别是4cm、6cm．则线段AB的中点C到直线l的距离是（　　）

A．1或5

B．3或5

C．4

D．5

Answer 1

（1）线段AB在直线l的同侧：
∵AN=4，BM=6，AN∥BN∥CD，C为AB的中点，
∴CD=

1

2

（AN+BM）=

1

2

（4+6）=5（cm）；

（2）线段AB在直线l的异侧：
连接NB，AM．延长CD交AM于E，反向延长CD交BN于F．
∵CD⊥NM，C为AB的中点，
∴EF为梯形AMBN的中位线．
∴EF=

1

2

（AN+BM）=

1

2

（4+6）=5．
在△ABN中，CF为中位线，∴CF=

1

2

AN=

1

2

×4=2．
同理，在△AMN中，DE=

1

2

AN=

1

2

×4=2．
故CD=EF-CF-ED=5-2-2=1（cm）．
故选A．