题目内容
如图1,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D=90°.
(1)如图2,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到点C停止,设P、Q同时从点B出发t秒时,△PBQ的面积为y1(cm2),求y1(cm2)关于t(秒)的函数关系式;
(2)如图3,动点P以每秒1cm的速度从点B出发沿BA运动,点E在线段CD上随之运动,且PC=PE.设点P从点B出发t秒时,四边形PADE的面积为y2(cm2),求y2(cm2)关于t(秒)的函数关系式,并写出自变量t的取值范围.

(1)如图2,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到点C停止,设P、Q同时从点B出发t秒时,△PBQ的面积为y1(cm2),求y1(cm2)关于t(秒)的函数关系式;
(2)如图3,动点P以每秒1cm的速度从点B出发沿BA运动,点E在线段CD上随之运动,且PC=PE.设点P从点B出发t秒时,四边形PADE的面积为y2(cm2),求y2(cm2)关于t(秒)的函数关系式,并写出自变量t的取值范围.

(1)过点A作AM⊥BC于M,如图1,则AM=6,BM=8,
∴AD=MC=2.
过点P作PN⊥BC于N,则△PNB∽△AMB,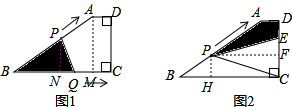
∴
=
.
∴
=
.
∴PN=
t.
①当点P在BA上运动时,
y1=
BQ•NP=
t•
t=
t2;
②当点P在AD上运动时,BQ=BC=10,PN=DC=6,
y1=
BQ•NP=
×10×6=30;
③当点P在DC上运动时,
y1=
BQ•CP=
×10(10+2+6-t)=-5t+90.
(2)过点P作PF⊥CD于F,PH⊥BC于H,如图2,
∵∠BCD=90°,
∴四边形PHCF是矩形,
∴FC=EF=PH=
t,
在Rt△BHP中,BH=
=
=
t,
∴PF=BC-HB=10-
t.
∴y2=S梯形ABCD-S△BPC-S△PEC=
(2+10)×6-
×10×
t-
×
t(10-
t)
=
t2-9t+36
当CE=CD时,
t=6,
∴t=5.
∴自变量t的取值范围是0≤t≤5.
∴AD=MC=2.
过点P作PN⊥BC于N,则△PNB∽△AMB,
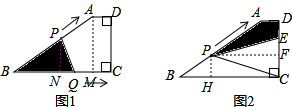
∴
| PN |
| AM |
| BP |
| BA |
∴
| PN |
| 6 |
| t |
| 10 |
∴PN=
| 3 |
| 5 |
①当点P在BA上运动时,
y1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 3 |
| 10 |
②当点P在AD上运动时,BQ=BC=10,PN=DC=6,
y1=
| 1 |
| 2 |
| 1 |
| 2 |
③当点P在DC上运动时,
y1=
| 1 |
| 2 |
| 1 |
| 2 |
(2)过点P作PF⊥CD于F,PH⊥BC于H,如图2,
∵∠BCD=90°,
∴四边形PHCF是矩形,
∴FC=EF=PH=
| 3 |
| 5 |
在Rt△BHP中,BH=
| BP2-PH2 |
t2-(
|
| 4 |
| 5 |
∴PF=BC-HB=10-
| 4 |
| 5 |
∴y2=S梯形ABCD-S△BPC-S△PEC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 5 |
| 1 |
| 2 |
| 6 |
| 5 |
| 4 |
| 5 |
=
| 12 |
| 25 |
当CE=CD时,
| 6 |
| 5 |
∴t=5.
∴自变量t的取值范围是0≤t≤5.

练习册系列答案
相关题目




