题目内容
如图,在等腰梯形ABCD中,AB∥CD,AD=BC,AC、BD是多角线,将△ABD沿AB对折到△ABE的位置.
(1)判断四边形AEBC是形状?
(2)试证明你判断的结论.
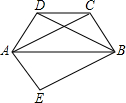
(1)判断四边形AEBC是形状?
(2)试证明你判断的结论.

答:四边形AEBC是平行四边形.
证明:在等腰梯形ABCD中,
∵AB∥CD,AD=BC,
∴AC=BD,
∵△ABD沿AB对折到△ABE的位置,
∴△ABD≌ABE,
∴AE=AD,BE=BD,
∴AE=BC,AC=BE,
∴四边形AEBC是平行四边形.
证明:在等腰梯形ABCD中,
∵AB∥CD,AD=BC,
∴AC=BD,
∵△ABD沿AB对折到△ABE的位置,
∴△ABD≌ABE,
∴AE=AD,BE=BD,
∴AE=BC,AC=BE,
∴四边形AEBC是平行四边形.

练习册系列答案
相关题目