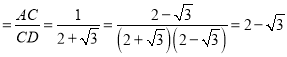题目内容
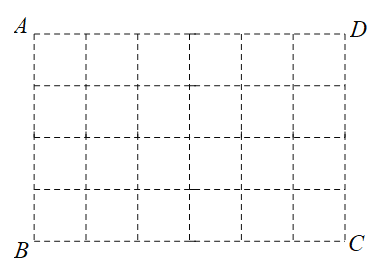
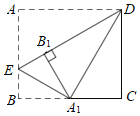
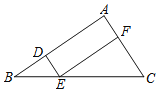
【题目】如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
(1)求证:△BDE∽△EFC.
(2)设![]() ,
,
①若BC=12,求线段BE的长;
②若△EFC的面积是20,求△ABC的面积.
【答案】(1)见解析;(2)①BE=4;②45
【解析】
(1)由平行线的性质得出∠DEB=∠FCE,∠DBE=∠FEC,即可得出结论;
(2)①由平行线的性质得出![]() =
=![]() =
=![]() ,即可得出结果;
,即可得出结果;
②先求出![]() =
=![]() ,易证△EFC∽△BAC,由相似三角形的面积比等于相似比的平方即可得出结果.
,易证△EFC∽△BAC,由相似三角形的面积比等于相似比的平方即可得出结果.
(1)证明:∵DE∥AC,
∴∠DEB=∠FCE,
∵EF∥AB,
∴∠DBE=∠FEC,
∴△BDE∽△EFC;
(2)解:①∵EF∥AB,
∴![]() =
=![]() =
=![]() ,
,
∵EC=BC﹣BE=12﹣BE,
∴![]() =
=![]() ,
,
解得:BE=4;
②∵![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵EF∥AB,
∴△EFC∽△BAC,
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,
,
∴S△ABC=![]() S△EFC=
S△EFC=![]() ×20=45.
×20=45.

 名校课堂系列答案
名校课堂系列答案【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
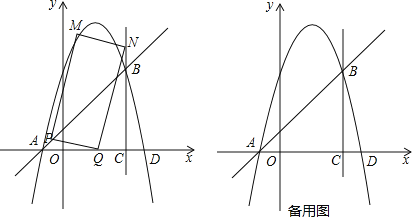
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
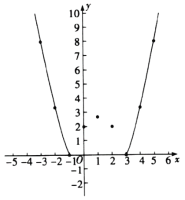
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程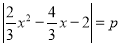 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.