题目内容
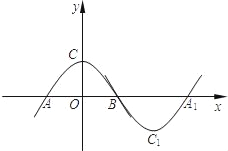
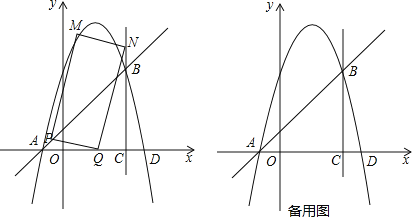
【题目】如图，抛物线y=﹣x2+bx+c和直线y=x+1交于A，B两点，点A在x轴上，点B在直线x=3上，直线x=3与x轴交于点C
（1）求抛物线的解析式；
（2）点P从点A出发，以每秒
个单位长度的速度沿线段AB向点B运动，点Q从点C出发，以每秒2个单位长度的速度沿线段CA向点A运动，点P，Q同时出发，当其中一点到达终点时，另一个点也随之停止运动，设运动时间为t秒（t＞0）．以PQ为边作矩形PQNM，使点N在直线x=3上．
①当t为何值时，矩形PQNM的面积最小？并求出最小面积；
②直接写出当t为何值时，恰好有矩形PQNM的顶点落在抛物线上．
【答案】（1）抛物线解析式为y=﹣x2+3x+4；（2）①当t=
时，面积最小是
；②t=
、
或2.
【解析】
（1）利用待定系数法进行求解即可；
（2）①分别用t表示PE、PQ、EQ，用△PQE∽△QNC表示NC及QN，列出矩形PQNM面积与t的函数关系式问题可解；
②由①利用线段中点坐标分别等于两个端点横纵坐标平均分的数量关系，表示点M坐标，分别讨论M、N、Q在抛物线上时的情况，并分别求出t值．
（1）由已知，B点横坐标为3，
∵A、B在y=x+1上，
∴A（﹣1，0），B（3，4），
把A（﹣1，0），B（3，4）代入y=﹣x2+bx+c得，
，解得：
，
∴抛物线解析式为y=﹣x2+3x+4；
（2）①如图，过点P作PE⊥x轴于点E，
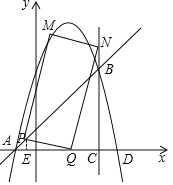
∵直线y=x+1与x轴夹角为45°，P点速度为每秒
个单位长度，
∴t秒时点E坐标为（﹣1+t，0），Q点坐标为（3﹣2t，0），
∴EQ=4﹣3t，PE=t，
∵∠PQE+∠NQC=90°，
∠PQE+∠EPQ=90°，
∴∠EPQ=∠NQC，
∴△PQE∽△QNC，
∴
，
∴矩形PQNM的面积S=PQNQ=2PQ2，
∵PQ2=PE2+EQ2，
∴S=2（
）2=20t2﹣48t+32，
当t=
时，
S最小=20×（）2﹣48×+32=；
②由①点Q坐标为（3﹣2t，0），P（﹣1+t，t），C（3，0），
∴△PQE∽△QNC，可得NC=2QE=8﹣6t，
∴N点坐标为（3，8﹣6t），
由矩形对边平行且相等，P（﹣1+t，t），Q （3﹣2t，0），
∴点M坐标为（3t﹣1，8﹣5t）
当M在抛物线上时，则有
8﹣5t=﹣（3t﹣1）2+3（3t﹣1）+4，
解得t=，
当点Q到A时，Q在抛物线上，此时t=2，
当N在抛物线上时，8﹣6t=4，
∴t=，
综上所述当t=、
或2时，矩形PQNM的顶点落在抛物线上．
