题目内容
【题目】某数学兴趣小组对函数![]() 的图象和性质进行了研究,探究过程如下.
的图象和性质进行了研究,探究过程如下.
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下.
x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 8 | m | 0 | 2 | n | 2 | 0 |
| 8 | … |
其中,m= ,n= ;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请补全函数图象的剩余部分;
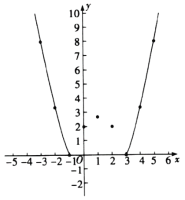
(3)进一步探究函数图象发现:
①函数图象与x轴有_____________个交点;
②方程![]() 有_____________个实数根;
有_____________个实数根;
③当关于x的方程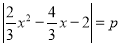 有3个实数根时,p的值是_____________.
有3个实数根时,p的值是_____________.
【答案】(1)![]() ;
;![]() ;(2)答案见解析;(3)①2;②4;③
;(2)答案见解析;(3)①2;②4;③![]()
【解析】
(1)代值计算即可;
(2)用光滑的曲线连接便可;
(3)根据函数图象利用数形结合法解答便可.
解:(1)将x=-2,y=m代入![]() 中,得m=
中,得m=![]() ,
,
将x=1,y=n代入![]() 中,得n=
中,得n=![]() ,
,
故答案为:![]() ;
;![]() ;
;
(2)用光滑的曲线连接得,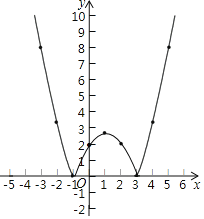
(3)①由函数图象可知,函数图象与x轴有两个交点,
故答案为2;
②如图,直线y=1与函数图象有4个交点,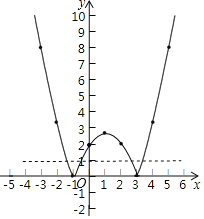
∴方程![]() 有4个实数根,
有4个实数根,
故答案为:4;
③当x=1时, ![]() =
=![]() ,
,
如图,直线y=与函数图象有3个交点,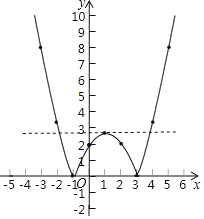
∴当关于x的方程![]() 有3个实数根时,p=
有3个实数根时,p=![]() ,
,
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】现代人对于健康越来越重视,比起去健身房或者运动量较大的户外活动,不少人更钟爱健步走.如今,在朋友圈里晒步数拼排行抢封面是不少人健步走的乐趣所在,“日行万步”已经成为众多运动爱好者的标配,在一次社会调查活动中,小李随机抽取某“健步走运动”团队20名成员,收集他们一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8752 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.
组别 | 步数分组 |
A |
|
B |
|
C |
|
D |
|
E |
|
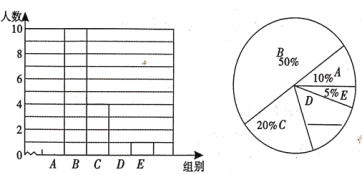
根据以上信息解答下列问题:
(1)补全两幅统计图;
(2)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;其中D组.数据的平均数 步;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.