题目内容
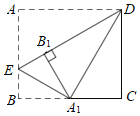
【题目】如图,在矩形ABCD中,E是AB上一点,将△ADE沿DE翻折,点A恰好落在BC上,记为A1,折痕为DE.再将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1.若AD=1,则AB的长为_____.
【答案】![]() .
.
【解析】
利用矩形的性质,证明∠ADE=∠A1DE=∠A1DC=30°,∠C=∠A1B1D=90°,推出△DB1A1≌△DCA1,CD=B1D,设AB=DC=x,由DE长度列出方程求得x便可.
∵四边形ABCD为矩形,
∴∠ADC=∠C=∠B=90°,AB=DC,
由翻折知,△AED≌△A1ED,△A1BE≌△A1B1E,∠A1B1E=∠B=∠A1B1D=90°,
∴∠AED=∠A1ED,∠A1EB=∠A1EB1,BE=B1E,
∴∠AED=∠A1ED=∠A1EB=![]() ×180°=60°,
×180°=60°,
∴∠ADE=90°﹣∠AED=30°,∠A1DE=90°﹣∠A1EB1=30°,
∴∠ADE=∠A1DE=∠A1DC=30°,
又∵∠C=∠A1B1D=90°,DA1=DA1,
∴△DB1A1≌△DCA1(AAS),
∴DC=DB1,
在Rt△AED中,
∠ADE=30°,AD=1,
∴AE=![]() ,DE=
,DE=![]()
设AB=DC=x,则BE=B1E=x﹣![]()
∵B1E+B1D=DE,
∴x+x﹣![]() ,
,
∴![]() ,
,
即AB=![]() .
.
故答案为:![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】现代人对于健康越来越重视,比起去健身房或者运动量较大的户外活动,不少人更钟爱健步走.如今,在朋友圈里晒步数拼排行抢封面是不少人健步走的乐趣所在,“日行万步”已经成为众多运动爱好者的标配,在一次社会调查活动中,小李随机抽取某“健步走运动”团队20名成员,收集他们一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8752 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.
组别 | 步数分组 |
A |
|
B |
|
C |
|
D |
|
E |
|
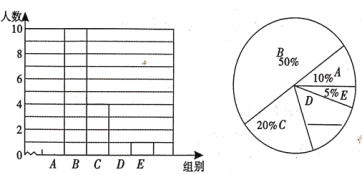
根据以上信息解答下列问题:
(1)补全两幅统计图;
(2)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;其中D组.数据的平均数 步;
(3)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.