��Ŀ����
����Ŀ����ͼ��������y=ax2+bx+c��a��0���ĶԳ���Ϊֱ��x=2���������߾���A����1��0����C��0����5�����㣬��x�ύ�ڵ�B��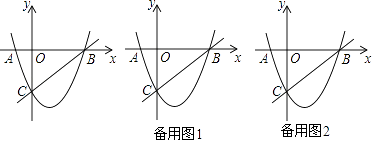
��1����ֱ��y=mx+n����B��C���㣬��ֱ��BC�������ߵĽ���ʽ��
��2�����PΪ�������ϵ�һ�����㣬����PB��PC������BPC����BCΪֱ�DZߵ�ֱ�������Σ����ʱ��P�����ꣻ
��3������������BC������һ������Q���Ե�QΪԲ������Q��ʹ�á�Q��ֱ��BC���У����˶��Ĺ������Ƿ����һ������Q�������ڣ���ֱ��д������Q�İ뾶���������ڣ���˵�����ɣ�
���𰸡�
��1��
�⣺�߶Գ���Ϊx=2���������߾���A����1��0����
��B��5��0����
��B��5��0����C��0����5���ֱ����y=mx+n�� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��BC�Ľ���ʽΪy=x��5��
��y=a��x��5����x+1�����ѵ�C���������ã���5a=��5����ã�a=1��
�������ߵĽ���ʽΪ��y=x2��4x��5
��2��
�⣺�ٹ���C��CP1��BC�����������ڵ�P1����ͼ��
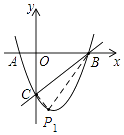
��ֱ��CP1�Ľ���ʽΪy=��x��5��
�� ![]() ����ã�
����ã� ![]() ����ȥ����
����ȥ���� ![]() ��
��
��P1��3����8����
�ڹ���B��BP2��BC������������P2����ͼ��
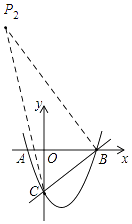
��BP2�Ľ���ʽΪy=��x+5��
�� ![]() ����ã�
����ã� ![]() ����ȥ����
����ȥ���� ![]() ��
��
��P2����2��7��
��3��
�⣺�������֪��Q�����BC��Զʱ���뾶���ƽ��ֱ��BC��ʹ����������ֻ��һ��������Q�������У�����ƽ�ƺ��ֱ�߽���ʽΪy=x+t��
�� ![]() ����ȥy������x2��5x��5��t=0��
����ȥy������x2��5x��5��t=0��
��=25+4��5+t��=0�����t=�� ![]() ��
��
��ƽ�ƺ�������������ʱ��ֱ�߽���ʽΪy=x�� ![]() ����Q��
����Q�� ![]() ����
���� ![]() ����
����
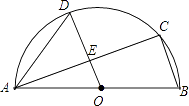
����QC��QB����QE��BC��E����ͼ��
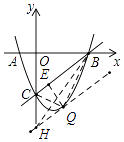
��ֱ��y=x�� ![]() ��y��Ľ���ΪH������HB��
��y��Ľ���ΪH������HB��
�� ![]() ��
��
��CH=��5������ ![]() ��=
��= ![]() ��
��
�� ![]() =
= ![]() ��
��
�� ![]() ��
��
�� ![]() ��BC=
��BC= ![]() ��
��
��QE= ![]() ��
��
�����뾶Ϊ ![]()
����������1�����ݶԳ��ἰA������ó�B�����꣬�Ӷ��ó�ֱ��BC����ʽ������A��B��C��������ó������߽���ʽ����2���ֱ��B��C������BC�Ĵ��ߣ��ó����ߵĽ���ʽ���������߽���ʽ�������P�㣻��3��ƽ��BC���������߸պ�����֮������ʱ���е㼴ΪQ�㣬��ʱQ���BC�ľ������Ҳ���ǰ뾶������ڳ��н�ûѧ�㵽ֱ�ߵľ��빫ʽ����ô��������õ���������д�������������y��Ľ���ΪH�����HBC���QBC�������ȣ�������������BCΪ�ף����BC���ϵĸ�Ϊ�𰸣�
�����㾫����������Ŀ����֪���������ö��κ����ĸ���Ͷ��κ�����ͼ������֪ʶ���Եõ�����Ĵ𰸣���Ҫ����һ��أ��Ա���x�������y֮��������¹�ϵ��һ��ʽ��y=ax2+bx+c(a��0��a��b��cΪ����)�����yΪx�Ķ��κ��������κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣮