题目内容
【题目】△ABC中,∠A=30°,∠B=45°,AC=4,求AB的长? 
【答案】解:过点C作CD⊥AB于D点, 在Rt△ADC中,∠A=30°,AC=4,
∴CD= ![]() AC=
AC= ![]() ×4=2,
×4=2,
∴AD= ![]() =
= ![]() =2
=2 ![]() ,
,
在Rt△CDB中,∠B=45°,CD=2,
∴CD=DB=2,
∴AB=AD+DB=2 ![]() +2.
+2.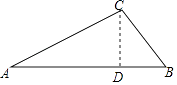
【解析】首先过点C作CD⊥AB于D点,由在Rt△ADC中,∠A=30°,AC=4,即可求得CD与AD的长,又由在Rt△CDB中,∠B=45°,即可求得BD的长,继而求得答案.
【考点精析】掌握解直角三角形是解答本题的根本,需要知道解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
【题目】已知二次函数y=x2﹣2x
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 0 | ﹣1 | … |
(1)请在表内的空格中填入适当的数;
(2)请在所给的平面直角坐标系中画出y=x2﹣2x的图象;
(3)当x再什么范围内时,y随x的增大而减小;
(4)观察y=x2﹣2x的图象,当x在什么范围内时,y>0.