题目内容
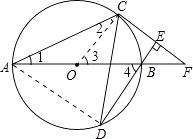
【题目】如图，AB为⊙O直径，C、D为⊙O上不同于A、B的两点，∠ABD=2∠BAC，连接CD．过点C作CE⊥DB，垂足为E，直线AB与CE相交于F点． 
（1）求证：CF为⊙O的切线；
（2）当BF=5，sinF= 
时，求BD的长．
【答案】
（1）证明：连接OC．
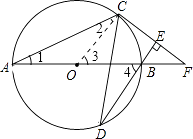
∵OA=OC，
∴∠1=∠2．
又∵∠3=∠1+∠2，
∴∠3=2∠1．
又∵∠4=2∠1，
∴∠4=∠3，
∴OC∥DB．
∵CE⊥DB，
∴OC⊥CF．
又∵OC为⊙O的半径，
∴CF为⊙O的切线；
（2）解：连结AD．
在Rt△BEF中，∵∠BEF=90°，BF=5，sinF= 
，
∴BE=BFsinF=3．
∵OC∥BE，
∴△FBE∽△FOC，
∴ 
．
设⊙O的半径为r，
∴ 
，
∴ 
．
∵AB为⊙O直径，
∴AB=15，∠ADB=90°，
∵∠4=∠EBF，
∴∠F=∠BAD，
∴ 
，
∴ 
，
∴BD=9．
【解析】（1）连接OC．先根据等边对等角及三角形外角的性质得出∠3=2∠1，由已知∠4=2∠1，得到∠4=∠3，则OC∥DB，再由CE⊥DB，得到OC⊥CF，根据切线的判定即可证明CF为⊙O的切线；（2）连结AD．先解Rt△BEF，得出BE=BFsinF=3，由OC∥BE，得出△FBE∽△FOC，则 ，设⊙O的半径为r，由此列出方程，解方程求出r的值，由AB为⊙O直径，得出AB=15，∠ADB=90°，再根据三角形内角和定理证明∠F=∠BAD，则由sin∠BAD= 
= ，求出BD的长．
【考点精析】利用切线的判定定理和相似三角形的判定与性质对题目进行判断即可得到答案，需要熟知切线的判定方法：经过半径外端并且垂直于这条半径的直线是圆的切线；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
