Question

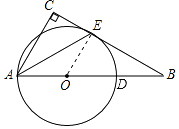
【题目】如图，Rt△ABC，∠C=90°，点D为AB上的一点，以AD为直径的⊙O与BC相切于点E，连接AE．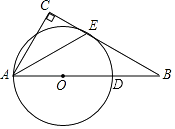
（1）求证：AE平分∠BAC；
（2）若AC=8，OB=18，求BD的长．

Answer 1

【答案】
（1）证明：如图，连接OE．

∵BC是⊙O切线，

∴OE⊥BC，

∴∠OEB=90°，

∵∠C=90°，

∴∠C=∠OEB=90°，

∴AC∥OE，

∴∠CAE=∠AEO，

∵OA=OE，

∴∠AEO=∠OAE=∠CAE，

∴AE平分∠CAB．

（2）解：设OE=OA=OD=r，

∵OE∥AC，

∴ = ，

∴ = ，

∴r=6（负根已经舍弃）

∴BD=OB﹣OD=18﹣6=12

【解析】（1）如图，连接OE．首先证明AC∥OE，推出∠CAE=∠AEO，由OA=OE，推出∠AEO=∠OAE=∠CAE即可证明．（2）设OE=OA=OD=r，由OE∥AC，得 = ，即 = ，解方程即可．
【考点精析】通过灵活运用切线的性质定理，掌握切线的性质：1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径即可以解答此题．