题目内容
【题目】定义：三角形一边的中线与这边上的高线之比称为这边上的中高比．
（1）直接写出等腰直角三角形腰上的中高比为 ．
（2）已知一个直角三角形一边上的中高比为5：4，求它的最小内角的正切值．
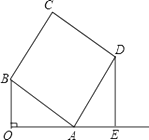
（3）如图，已知函数y= 
（x+4）（x﹣m）与x轴交于A、B两点，与y轴的负半轴交于点C，对称轴与x的正半轴交于点D，若△ABC中AB边上的中高比为5：4，求m的值．
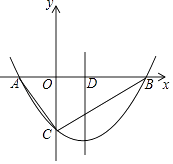
【答案】
（1）
（2）
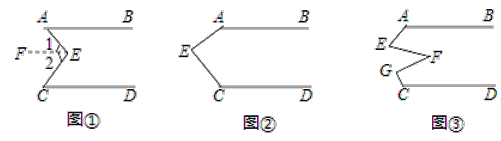
解：①当斜边上的中高比为5：4时，设高线为4k，则此边上的中线为5k，如图2，
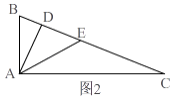
在△ABC中，∠BAC=90°，
∴AD是高，
∴AD=4x，AE是中线，
∴CE=AE=5x，
在RtADE中，DE= 
=3k，
∴CD=CE+DE=8k，
∴tan∠C= 
= 
= 
，
当直角边上的中高比为5：4时，设高为4k，此边上的中线为5k，
如图3，
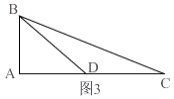
在△ABC中，∠BAC=90°，AB是AC边上的高，为4k，BD为AC边上的中线，为5k，
根据勾股定理得，AD= 
=3k，
∴AC=2AD=6k，
∴tan∠C= 
= 
，
∴直角三角形的最小内角的正切值为 或 ；
（3）
解：∵函数y= 
（x+4）（x﹣m）与x轴交于A、B两点，
∴令y=0，∴0= （x+4）（x﹣m），
∴x=﹣4或x=m，
∴A（﹣4，0），B（m，0），
∵点C是抛物线与y轴的交点，
∴C（0，﹣ 
），
∵对称轴与x的正半轴交于点D，
∴D（ 
，0），
在Rt△COD中，设CD=5k，
∴OC=4k，
根据勾股定理得，OD=3k，
∴ 
，∴ 
，
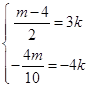即m的值为10．
【解析】解：（1）如图1，
设等腰直角三角形的直角边为2x，
∴BC边上的高为AB=2x，
∵AD是BC边上的中线，
∴BD= BC=x，
在Rt△ABD中，根据勾股定理得，AD= 
= 
x，
∴等腰直角三角形腰上的中高比为 
= ，
所以答案是： ；
