题目内容
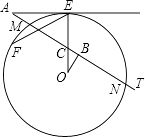
【题目】如图，AB为⊙O的内接正多边形的一边，已知∠OAB=70°，则这个正多边形的内角和为 ． 
【答案】1260°
【解析】解：∵OA=OB， ∴∠OAB=∠OBA=70°，
∴∠AOB=40°，
∵AB为⊙O的内接正多边形的一边，
∴正多边形的边数= 
=9，
∴这个正多边形的内角和=（9﹣2）×180°=1260°，
所以答案是：1260°．
【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识，掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°，以及对正多边形和圆的理解，了解圆的内接四边形的对角互补，并且任何一个外角都等于它的内对角；圆的外切四边形的两组对边的和相等．
练习册系列答案
目标测试系列答案
相关题目
