��Ŀ����
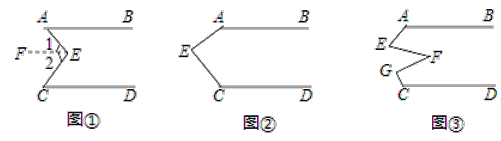
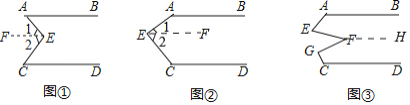
����Ŀ������֪����ͼ����AB��CD����E��ֱ��AB��CD֮�䣬����AE��BE����˵����BEE+��DCE����AEC����������������Ľ�����̣����������Ľ�����̣�����գ����ɻ���ѧʽ����
�⣺��ͼ�٣�����E��EF��AB
���BAE����1���� ����
��AB��CD���� ����
��CD��EF���� ����
���2����DCE
���BAE+��DCE����1+��2���� ����
���BAE+��DCE����AEC
��̽��������E����ͼ�ڵ�λ��ʱ�������������䣬��˵����AEC+��FGC+��DCE��360�㣻
��Ӧ�ã���E��F��G��ֱ��AB��CD֮�䣬����AE��EF��FG��CG�������������䣬��ͼ�ۣ�����EFG��36�������BAE+��AEF+��FGC+��DCG���� ���㣮
���𰸡�����֪����ֱ��ƽ���ڴ�����ȣ���֪��ƽ����ͬһֱ�ߵ�����ֱ��ƽ�У���ʽ�����ʣ���̽����360�㣻��Ӧ�á�396��
��������
�ڽ�����ʱ, ����E��EF��AB, ��AB��CD, ���ɵ�AB��EF��CD, Ȼ�������ֱ��ƽ��, ͬ���ڽǻ���, ������ô�.
�⣺����֪��
��ͼ�٣�����![]() ��
��![]()
![]() ����ֱ��ƽ���ڴ�����ȣ�
����ֱ��ƽ���ڴ�����ȣ�
![]() ����֪��
����֪��
![]() ��ƽ����ͬһֱ�ߵ�����ֱ��ƽ�У�
��ƽ����ͬһֱ�ߵ�����ֱ��ƽ�У�
![]()
![]() ����ʽ�����ʣ�
����ʽ�����ʣ�
![]() ��
��
�ʴ�Ϊ����ֱ��ƽ���ڴ�����ȣ���֪��ƽ����ͬһֱ�ߵ�����ֱ��ƽ�У���ʽ�����ʣ�
��̽����
��ͼ2�У���![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
��Ӧ�á�
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]()
�ʴ�Ϊ396��