Question

【题目】如图，已知OA⊥OB，OA=4，OB=3，以AB为边作矩形ABCD，使AD=a，过点D作DE垂直OA的延长线交于点E．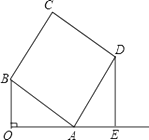
（1）证明：△OAB∽△EDA；
（2）当a为何值时，△OAB与△EDA全等？请说明理由，并求出此时点C到OE的距离．

Answer 1

【答案】
（1）证明：如图所示，

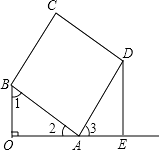
∵OA⊥OB，

∴∠1+∠2=90°，

又∵四边形ABCD是矩形，

∴∠BAD=90°，

∴∠2+∠3=90°，

∴∠1=∠3，

∵OA⊥OB，OE⊥OA，

∴∠BOA=∠DEA=90°，

∴△OAB∽△EDA．

（2）解：在Rt△OAB中，AB= =5，

由（1）可知∠1=∠3，∠BOA=∠DEA=90°，

∴当a=AD=AB=5时，△AOB与△EDA全等．

当a=AD=AB=5时，可知矩形ABCD为正方形，

∴BC=AB，如图，过点C作CH⊥OE交OE于点H，

则CH就是点C到OE的距离，过点B作BF⊥CH交CH于点F，

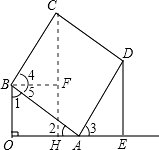
则∠4与∠5互余，∠1与∠5互余，

∴∠1=∠4，

又∵∠BFC=∠BOA，BC=AB，

∴△OAB≌△FCB（AAS），

∴CF=OA=4，BO=BF．

∴四边形OHFB为正方形，

∴HF=OB=3，

∴点C到OE的距离CH=CF+HF=4+3=7．

【解析】（1）由于四边形ABCD是矩形，则∠BAD=90°，那么∠OBA、∠DAE同为∠BAO的余角，即∠OBA=∠DAE，而∠BOA、∠DEA都是直角，由此可证得△OAB∽△EDA．（2）若△OAB与△EDA全等，则AB=AD，在Rt△OAB中，利用勾股定理易求得AB=5，那么a=AD=AB=5； 求C到OE的距离，可过C作CH⊥OE于H，过B作BF⊥CH于F；那么CH就是所求的距离，通过上面的解题思路，易证得△CBF≌△ABO，得CH=OA=4，BO=BF，那么四边形BOHF是正方形，由此可得FH=BO=3，根据CH=CF+FH即可求得C到OE的距离．
【考点精析】通过灵活运用矩形的性质和相似三角形的判定，掌握矩形的四个角都是直角，矩形的对角线相等；相似三角形的判定方法:两角对应相等，两三角形相似（ASA）；直角三角形被斜边上的高分成的两个直角三角形和原三角形相似； 两边对应成比例且夹角相等，两三角形相似（SAS）；三边对应成比例，两三角形相似（SSS）即可以解答此题．