题目内容
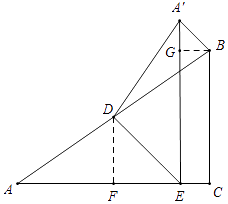
【题目】如图,在△ABC中,∠C=90°,AB=5,BC=3,D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A'处,当A'E⊥AC时,A'B= . 
【答案】![]()
【解析】解:∵在△ABC中,∠C=90°,AB=5,BC=3, ∴AC=4,
由折叠可得∠AED=∠A'ED,
当A'E⊥AC时,∠AED=∠A'ED=45°,
如图,过D作DF⊥AC于F,过B作BG⊥A'E于G,则△DEF是等腰直角三角形,
∵DF∥BC,D是AB的中点,BC=3,
∴AF=CF= ![]() AC=2,DF=
AC=2,DF= ![]() BC=
BC= ![]() ,
,
∴EF= ![]() ,CE=2﹣
,CE=2﹣ ![]() =
= ![]() ,
,
∴矩形BCEG中,BG=CE= ![]() ,BC=EG=3,
,BC=EG=3,
∵AE=2+ ![]() =
= ![]() ,
,
∴A'E= ![]() ,
,
∴A'G= ![]() ﹣3=
﹣3= ![]() ,即A'G=BG,
,即A'G=BG,
∴等腰Rt△A'BG中,A'B= ![]() BG=
BG= ![]() .
.
所以答案是: ![]() .
.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.

【题目】问题情境
已知矩形的面积为S(S为常数,S>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
数学模型
设该矩形的长为x,周长为y,则y与x的函数关系式为y=2(x+ ![]() )(x>0)
)(x>0)
探索研究
(1)我们可以借鉴学习函数的经验,先探索函数y=x+ ![]() (x>0)的图象性质.
(x>0)的图象性质.
①列表:
x | … |
|
|
| 1 | 2 | 3 | 4 | … |
y | … |
| m |
| 2 |
|
|
| … |
表中m=;
②描点:如图所示;
③连线:请在图中画出该函数的图象;
④观察图象,写出两条函数的性质;
(2)解决问题
在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.同样通过配方也可以求函数y=x+ ![]() (x>0)的最小值.
(x>0)的最小值.
y=x+ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() ﹣2
﹣2 ![]()
![]() +2
+2 ![]()
![]() =
= ![]() +2
+2
∵ ![]() ≥0,∴y≥2
≥0,∴y≥2
∴当 ![]() ﹣
﹣ ![]() =0,即x=1时,y最小值=2
=0,即x=1时,y最小值=2
请类比上面配方法,直接写出“问题情境”中的问题答案.


