题目内容
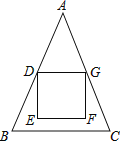
【题目】如图,△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC的距离为( )
A.1B.2C.12![]() ﹣6D.6
﹣6D.6![]() ﹣6
﹣6
【答案】D
【解析】
首先过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H,易证得△ADG∽△ABC,然后根据相似三角形的性质以及正方形的性质求解即可求得答案.
解:过点A作AM⊥BC于点M,交DG于点N,延长GF交BC于点H,
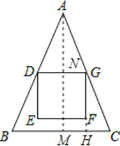
∵AB=AC,AD=AG,
∴AD:AB=AG:AC,
∵∠BAC=∠DAG,
∴△ADG∽△ABC,
∴∠ADG=∠B,
∴DG∥BC,
∵四边形DEFG是正方形,
∴FG⊥DG,GF=DG=6,
∴FH⊥BC,AN⊥DG,
∵AB=AC=18,BC=12,
∴BM=![]() BC=6,
BC=6,
∴AM=![]() =12
=12![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AN=6![]() ,
,
∴MN=AM﹣AN=6![]() ,
,
∴FH=MN﹣GF=6![]() ﹣6.
﹣6.
故选:D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目