题目内容
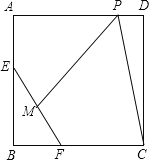
【题目】如图，在边长为8的正方形ABCD中，E、F分别是边AB、BC上的动点，且EF＝6，M为EF中点，P是边AD上的一个动点，则CP+PM的最小值是_____．
【答案】8
﹣3
【解析】
延长CD到C'，使C'D=CD，CP+PM=C'P+PM，当C'，P，M三点共线时，C'P+PM的值最小，根据题意，点M的轨迹是以B为圆心，3为半径的圆弧上，圆外一点C'到圆上一点M距离的最小值C'M=C'B﹣3，根据勾股定理即可得到结论．
延长CD到C'，使C'D=CD．
∵PD⊥CD，∴PD是CC'的垂直平分线，∴CP=C'P，则CP+PM=C'P+PM，当C'，P，M三点共线时，C'P+PM的值最小，根据题意，点M的轨迹是以B为圆心，3为半径的圆弧上，圆外一点C'到圆上一点M距离的最小值C'M=C'B﹣3．
∵BC=CD=8，∴CC'=16，∴C'D=
=8，∴CP+PM的最小值是
．
故答案为：．
练习册系列答案
阅读快车系列答案
相关题目
