题目内容
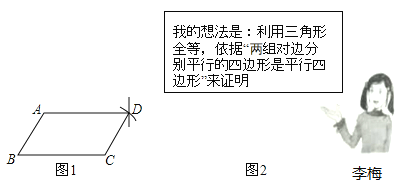
【题目】李梅同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形![]() ,并写出了如下不完整的已知和求证.
,并写出了如下不完整的已知和求证.
已知:如图1,在四边形![]() 中,
中,![]() ,
,![]()
求证:四边形![]() 是 四边形.
是 四边形.
(1)填空,补全已知和求证;
(2)按李梅的想法写出证明.
【答案】(1)CD;平行;(2)证明见解析.
【解析】
(1)命题的题设为“两组对边分别相等的四边形”,结论是“是平行四边形”,根据题设可得已知:在四边形ABCD中,BC=AD,AB=CD,求证:四边形ABCD是平行四边形;
(2)连接BD,利用SSS定理证明△ABD≌△CDB可得∠ADB=∠DBC,∠ABD=∠CDB,进而可得AB∥CD,AD∥CB,根据两组对边分别平行的四边形是平行四边形可得四边形ABCD是平行四边形;
解:(1)已知:如图1,在四边形![]() 中,
中,![]()
求证:四边形![]() 是平行四边形.
是平行四边形.

(2)证明:连接![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
![]()
![]()
![]()
∴四边形![]() 是平行四边形;
是平行四边形;
故答案为:CD,平行.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目