题目内容
【题目】如图，要在平行四边形
内作一个菱形.甲，乙两位同学的作法分别如下：
对于甲乙两人的作法，可判断（ ）
A.甲正确，乙错误B.甲错误，乙正确C.甲，乙均正确D.甲、乙均错误
【答案】C
【解析】
甲：首先证明△AOE≌△COF（ASA），可得AE=CF，再根据一组对边平行且相等的四边形是平行四边形可判定四边形AECF是平行四边形，再由AC⊥EF，可根据对角线互相垂直的四边形是菱形判定出AECF是菱形；乙：四边形ABCD是平行四边形，可根据角平分线的定义和平行线的定义，求得AB=AF，所以四边形ABEF是菱形.
甲的作法正确，
证明：∵四边形ABCD是平行四边形，
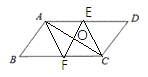
∴AD∥BC，
∴∠DAC=∠ACB，
∵EF是AC的垂直平分线，
∴AO=CO，
在△AOE和△COF中，
，
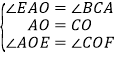∴△AOE≌△COF（ASA），
∴AE=CF，
又∵AE∥CF，
∴四边形AFCE是平行四边形，
∵EF⊥AC，
∴四边形AFCE是菱形；
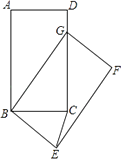
乙的作法正确；
证明：∵AD∥BC，
∴∠1=∠2，∠6=∠7，
∵BF平分∠ABC，AE平分∠BAD，
∴∠2=∠3，∠5=∠6，
∴∠1=∠3，∠5=∠7，
∴AB=AF，AB=BE，
∴AF=BE，
∵AF∥BE，且AF=BE，
∴四边形ABEF是平行四边形，
∵AB=AF，
∴平行四边形ABEF是菱形；
故甲、乙做法均正确.
故选C.
练习册系列答案
相关题目
