题目内容
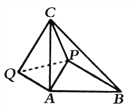
【题目】如图,在等腰ΔABC中,∠CAB=90°AB=AC,P为ΔABC内的一点,且PA=AQ=1,CQ=BP=3,CP=![]() ,求∠APC的大小.(提示:连接PQ)
,求∠APC的大小.(提示:连接PQ)
【答案】135°.
【解析】
试题由于△ABC为等腰直角三角形,AB=AC,则把△APB绕A点逆时针旋转90°可得到△AQC,连PQ,根据旋转的性质得到∠QAP=90°,QA=PA=1,QC=PB=3,得到△PAQ为等腰直角三角形,根据等腰直角三角形的性质得QP=![]() PA=
PA=![]() ,∠APQ=45°,在△QPC中,可得到PC2+QP2=QC2,根据勾股定理的逆定理得到△QPC为直角三角形,∠CPQ=90°,利用∠CPA=∠CPQ+∠APP′进行计算即可.
,∠APQ=45°,在△QPC中,可得到PC2+QP2=QC2,根据勾股定理的逆定理得到△QPC为直角三角形,∠CPQ=90°,利用∠CPA=∠CPQ+∠APP′进行计算即可.
试题解析:∵△ABC为等腰直角三角形,AB=AC,
∴把△APB绕A点逆时针旋转90°可得到△AQC,连PQ,如图,

∴∠QAP=90°,QA=PA=1,QC=PB=3,
∴△PAQ为等腰直角三角形,
∴QP=![]() PA=
PA=![]() ,∠APQ=45°,
,∠APQ=45°,
在△QPC中,QC=3,QP=![]() ,PC=
,PC=![]() ,
,
∵(![]() )2+(
)2+(![]() )2=32,
)2=32,
∴PC2+QP2=QC2,
∴△QPC为直角三角形,∠CPQ=90°,
∴∠CPA=∠CPQ+∠APQ=90°+45°=135°.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目