题目内容
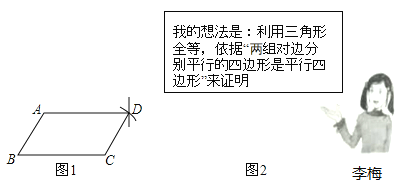
【题目】已知如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 分别是
分别是![]() 的中点,分别延长
的中点,分别延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是矩形;
是矩形;
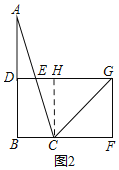
(2)如图2,连接![]() ,若
,若![]() 平分
平分![]() .
.
①求![]() 的长;
的长;
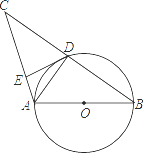
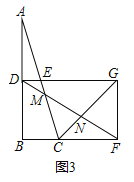
②如图3,连接![]() ,分别交
,分别交![]() 于点
于点![]() .求证:
.求证:![]() 是等腰三角形.
是等腰三角形.

【答案】(1)证明见解析;(2)①5;②证明见解析.
【解析】
(1)根据一组对边平行且相等可得:四边形DBFG是平行四边形,根据有一个角是直角的平行四边形是矩形可得结论;
(2)①如图2,过C作CH⊥DG于H,证明△ADE≌△CHE,得CH=AD,EH=DE,设CF=x,则BF=2+x,GH=CF=x,EG=x+1,根据平行线的性质和角平分线的定义得:EG=CG=x+1,结合勾股定理列方解方程可得结论;
②证明△DEM∽△FCM,得![]() 根据勾股定理计算AC、DF、CG的长,再结合
根据勾股定理计算AC、DF、CG的长,再结合![]() 可得MN=CM,得△MCN是等腰三角形.
可得MN=CM,得△MCN是等腰三角形.
证明:(1)如图1,∵点![]() 分别是
分别是![]() 的中点,
的中点,
![]()
![]()
![]()
∴四边形![]() 是平行四边形,
是平行四边形,
![]()
∴![]() 是矩形;
是矩形;
(2)①如图2,过![]() 作
作![]() 于
于![]() ,
,
![]()
![]() ,
,
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
∵![]() 平分
平分![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]()
![]()
![]()
②如图![]() :
: ![]() ,
,
![]()
![]() ,
,
由勾股定理得:![]() ,
,
![]() ,
,
![]() ,
,
![]() 是
是![]() 的中点,
的中点,
![]() ,
,
![]() ,
,
同理得:![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 是等腰三角形.
是等腰三角形.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目