Question

【题目】已知函数

（1）m= 时，函数图像与x轴只有一个交点；

（2）m为何值时，函数图像与x轴没有交点；

（3）若函数图像与x轴交于A、B两点，与y轴交于点C，且△ABC的面积为4，求m的值.

Answer 1

【答案】(1) 或；(2) ；(3) .

【解析】试题分析：（1）分两种情况进行讨论：①当m－1＝0时，函数是一次函数，图象是直线，与x轴有一个交点；②当m－1≠0时，函数是二次函数，令根的判别式等于0，求出m的值，即可得到结果；

（2）令根的判别式小于0即可求出m的范围；

（3）对于二次函数解析式，分别令x与y为0求出y与x的值，利用根与系数的关系求出两个之和与两根之积，表示出三角形ABC的面积，根据已知面积为4即可求出m的值．

试题解析：

解：（1）分两种情况进行讨论：

①当m－1＝0，m＝1时，函数是一次函数y＝2x，图象是直线，与x轴有一个交点；

②当m－1≠0，m≠1时，函数是二次函数，

∵函数y＝(m－1)x2＋2mx＋m－1图象与x轴只有一个交点，

∴△＝4m2－4（m－1）2＝4m2－4m2＋8m－4＝0，

解得：m＝.

故答案为1或；

（2）∵函数与x轴没有交点，

∴△＝4m2－4（m－1）2＝4m2－4m2＋8m－4＜0，即m＜；

（3）对于二次函y＝(m－1)x2＋2mx＋m－1，

令x＝0，得到y＝m－1，即C（0，m－1），

令y＝0，得到(m－1)x2＋2mx＋m－1＝0，

设此方程的两根为a，b，

∴由根与系数的关系得到a＋b＝， ab＝1，

∴AB＝|a－b|＝＝＝ ，

∵△ABC的面积为4，

∴AByC纵坐标＝4，即|m－1|×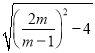＝8，

两边平方得：4m2－4(m－1)2＝64，即8m＝68，

解得：m＝．