题目内容
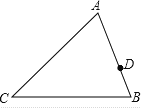
【题目】如图,AD是△ABC的角平分线,线段AD的垂直平分线分别交AB和AC于点E、F,连接DE、DF.
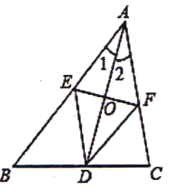
(1)试判定四边形AEDF的形状,并证明你的结论.
(2)若DE=13,EF=10,求AD的长.
(3)△ABC满足什么条件时,四边形AEDF是正方形?
【答案】(1)四边形AEDF是菱形,证明见解析;(2)24;(3)当△ABC中∠BAC=90°时,四边形AEDF是正方形;
【解析】(1)由∠BAD=∠CAD,AO=AO,∠AOE=∠AOF=90°证△AEO≌△AFO,推出EO=FO,得出平行四边形AEDF,根据EF⊥AD得出菱形AEDF;
(2)由(1)知菱形AEDF对角线互相垂直平分,故EO=![]() EF=5,根据勾股定理得DO=12,从而得到AD=24;
EF=5,根据勾股定理得DO=12,从而得到AD=24;
(3)根据有一个角是直角的菱形是正方形可得∠BAC=90°时,四边形AEDF是正方形.
(1)四边形AEDF是菱形,
∵AD平分∠BAC,
∴∠1=∠2,
又∵EF⊥AD,
∴∠AOE=∠AOF=90°
∵在△AEO和△AFO中
∵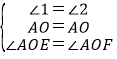 ,
,
∴△AEO≌△AFO(ASA),
∴EO=FO,
∵EF垂直平分AD,
∴EF、AD相互平分,
∴四边形AEDF是平行四边形
又EF⊥AD,
∴平行四边形AEDF为菱形;
(2)由(1)知,EO=![]() EF=5,AD=2DO,
EF=5,AD=2DO,
在Rt△DOE中,∵DE=13,EO=5
∴DO=![]() ,
,
∴AD=2DO=24;
(3)当△ABC中∠BAC=90°时,四边形AEDF是正方形;
∵∠BAC=90°,
∴四边形AEDF是正方形(有一个角是直角的菱形是正方形).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目