题目内容
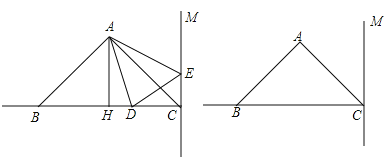
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
【答案】(1)3t,t;(2)t为![]() s或
s或![]() s;(3)见解析.
s;(3)见解析.
【解析】
(1)根据路程=速度×时间,即可得出结果;
(2)首先求出△ABD中BD边上的高,然后根据面积公式列出方程,求出BD的值,分两种情况分别求出t的值即可;
(3)假设△ABD≌△ACE,根据全等三角形的对应边相等得出BD=CE,分别用含t的代数式表示CE和BD,得到关于t的方程,从而求出t的值.
(1)根据题意得:CD=3tcm,CE=tcm;
故答案为:3t,t;
(2)∵S△ABD![]() BDAH=12,AH=4,
BDAH=12,AH=4,
∴AH×BD=24,
∴BD=6.
若D在B点右侧,则CD=BC﹣BD=2,t![]() ;
;
若D在B点左侧,则CD=BC+BD=14,t![]() ;
;
综上所述:当t为![]() s或
s或![]() s时,△ABD的面积为12 cm2;
s时,△ABD的面积为12 cm2;
(3)动点E从点C沿射线CM方向运动2秒或当动点E从点C沿射线CM的反向延长线方向运动4秒时,△ABD≌△ACE.
理由如下:
①当E在射线CM上时,D必在CB上,则需BD=CE.如图所示,
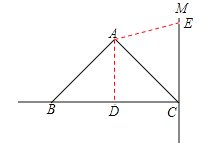
∵CE=t,BD=8﹣3t
∴t=8﹣3t,
∴t=2,
∵在△ABD和△ACE中,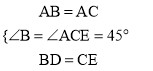 ,
,
∴△ABD≌△ACE(SAS).
②当E在CM的反向延长线上时,D必在CB延长线上,则需BD=CE.如图,
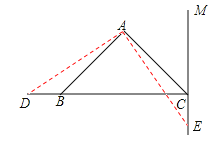
∵CE=t,BD=3t﹣8,
∴t=3t﹣8,
∴t=4,
∵在△ABD和△ACE中,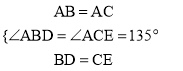 ,
,
∴△ABD≌△ACE(SAS).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案