题目内容
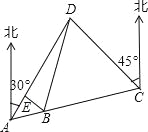
【题目】某市开展一项自行车旅游活动,线路需经A、B、C、D四地,如图,其中A、B、C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27,![]() )
)

【答案】从A地跑到D地的路程约为47m
【解析】
试题分析:求出∠DCA的度数,再判断出BC=CD,据此即可判断出△BCD是等边三角形.过点B作BE⊥AD,垂足为E,求出∠DAC的度数,利用三角函数求出AB的长,从而得到AB+BC+CD的长.
试题解析:由题意可知∠DCA=180°﹣75°﹣45°=60°,
∵BC=CD,
∴△BCD是等边三角形.
过点B作BE⊥AD,垂足为E,如图所示:
由题意可知∠DAC=75°﹣30°=45°,
∵△BCD是等边三角形,
∴∠DBC=60° BD=BC=CD=20km,
∴∠ADB=∠DBC﹣∠DAC=15°,
∴BE=sin15°BD≈0.25×20≈5m,
∴AB=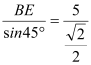 ≈7m,
≈7m,
∴AB+BC+CD≈7+20+20≈47m.
答:从A地跑到D地的路程约为47m.

练习册系列答案
相关题目