Question

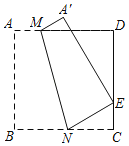
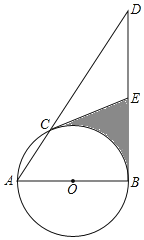
【题目】如图，将正方形ABCD沿AE，AF折叠后，点B、D恰好重合于点G，测得CF=1，∠CFE=60°，则正方形的边长是_______．

Answer 1

【答案】

【解析】

由CF=1，∠CFE=60°，得CE=，EF=2，由折叠可知，EG=BE，FG=FD，所以BE+FD=EG+GF=EF=2，因此求得BC+CD的长，即可求解．

∵正方形ABCD，
∴∠B=∠C=∠D=90°，AB=BC=CD=AD，
∵CF=1，∠CFE=60°，

∴∠CEF=30°，
∴CE=CF=，EF=2CF=2，
由折叠可知，EG=BE，FG=FD，
∴BE+FD=EG+GF=EF=2，
∴BC+CD=(BE+FD)+(CE+CF)=2+(1+)=3+，

∴BC=CD=．
故答案为：．