题目内容
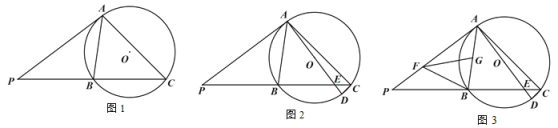
【题目】如图,矩形 ABCD 的对角线 AC 与 BD 交于点 O,点 E 在 AD 上,且 DE=CD,连接 OE,BE, ABE ![]() ACB ,若 AE=2,则 OE 的长为___________.
ACB ,若 AE=2,则 OE 的长为___________.
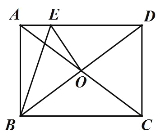
【答案】![]()
【解析】
作∠ACB的平分线CG交BE于G,AC与BE交于点F,首先证明CB=CF,AF=AE=2,然后在Rt△ABC中利用勾股定理构建方程求出DE=CD=AB=6,BC=CF=AD=8,BD=AC=10,过点E作EH⊥BD于H,证明△EHD∽△BAD,利用相似三角形的性质求出EH和DH,进而可得OH,再利用勾股定理求OE即可.
解:作∠ACB的平分线CG交BE于G,AC与BE交于点F,
∵ABE=![]() ACB,GCB=
ACB,GCB=![]() ACB,
ACB,
∴ABE=GCB,
∵ABE+∠EBC=90°,
∴GCB+∠GBC=90°,
∴CG⊥BE,
∵CG平分∠ACB,
∴CB=CF,
∴∠FBC=∠BFC=∠AFE,
∵AD∥BC,
∴∠AEF=∠FBC,
∴∠AEF=∠AFE,
∴AF=AE=2,
设DE=CD=AB=x,则BC=CF=AD=x+2,AC=x+2+2=x+4,
在Rt△ABC中,AB2+BC2=AC2,即x2+(x+2)2=(x+4)2,
解得:x=6(负值已舍去),
∴DE=CD=AB=6,BC=CF=AD=8,BD=AC=10,
过点E作EH⊥BD于H,
∵∠EHD=∠BAD,∠EDH=∠BDA,
∴△EHD∽△BAD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴OH=OD-DH=![]() BD-DH=
BD-DH=![]() ,
,
∴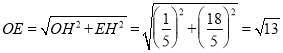 ,
,
故答案为:![]() .
.

 教材全解字词句篇系列答案
教材全解字词句篇系列答案【题目】每年4月23日是世界读书日,某校为了解学生课外阅读情况,随机抽取![]() 名学生,对每人每周用于课外阅读的平均时间(单位:
名学生,对每人每周用于课外阅读的平均时间(单位:![]() )进行调查,过程如下:
)进行调查,过程如下:
收集数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理数据:
课外阅读平均时间 |
|
|
|
|
等级 |
|
|
|
|
人数 |
|
|
|
|
分析数据:
平均数 | 中位数 | 众数 |
|
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)已知该校学生![]() 人,若每人每周用于课外阅读的平均时间不少于
人,若每人每周用于课外阅读的平均时间不少于![]() 为达标,请估计达标的学生数;
为达标,请估计达标的学生数;