题目内容
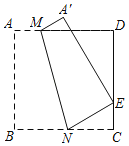
【题目】如图,把正方形纸片ABCD沿对边上的两点M、N所在的直线对折,使点B落在边CD上的点E处,折痕为MN,其中CE=![]() CD.若AB的长为2,则MN的长为( )
CD.若AB的长为2,则MN的长为( )
A.3B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
连接BE,作MG⊥BC于G,则MG=AB=BC=2,∠NMG+∠MNG=90°,由折叠的性质得:BE⊥MN,证明△MNG≌△EBC得出MN=BE,在Rt△BCE中,由勾股定理求出BE,即可得出结果.
连接BE,作MG⊥BC于G,如图所示:
则MG=AB=2,∠NMG+∠MNG=90°,
∵四边形ABCD是正方形,
∴BC=CD=AB=2,∠A=∠B=∠C=90°,
由折叠的性质得:BE⊥MN,
∴∠EBC+∠MNG=90°,
∴∠NMG=∠EBC,
在△MNG和△EBC中,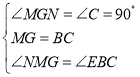 ,
,
∴△MNG≌△EBC(ASA),
∴MN=BE,
在Rt△BCE中,CE=![]() CD=
CD=![]() ,
,
由勾股定理得:BE=![]() =
=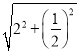 =
=![]() ,
,
∴MN=![]() ;
;

故选:B.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目